Harmonic Oscillation

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다만… 미분방정식은 졸업시험 대상 과목이 아니라는 걸 나중에 알게 되었습니다… OTL… 그래도 이왕 시작한 거 다시 복습 좀 해봅시다! 🏃 미분방정식 포스트 전체 보기

들어가며

본인은 개인적으로 “물리” 과목이랑 잘 안 맞는 것 같아서, 수학 공부할 때 물리 내용 나오는 것들은 대충 넘기는 버릇이 있습니다…. 그런데 미방을 공부해보니… 생각보다 물리로 설명하면 이해하기 쉬워지는 경험을 하게 된 것 같습니다 드디어

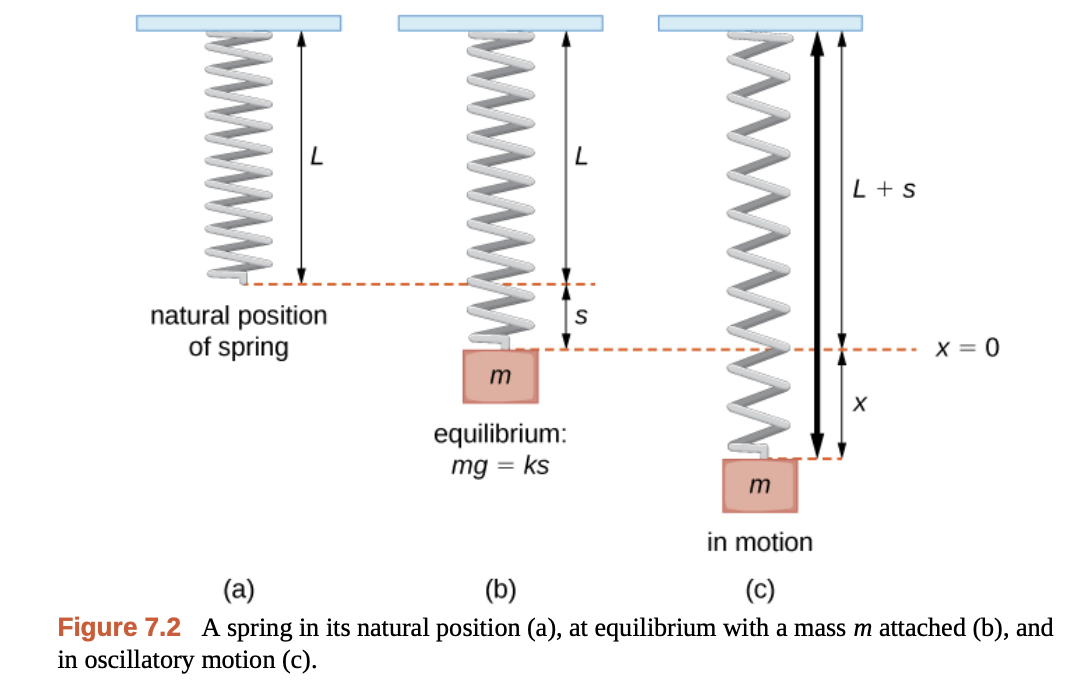G. Strange - CalculusVolume3-OP

그런 점에서 Harmonic Oscillation은 2차 미분방정식을 가장 쉽게 설명할 수 있는 도구인 것 같습니다. 잘 와닿기도 하고 상상하기도 쉽습니다.

Simple Harmonic Oscillation

\[x'' + kx = 0\]

조화 진동자에서 가장 간단한 상황입니다. 위의 Fig 7.2의 상황으로 물체의 변위 $x$에 따라 작용하는 용수철 힘 $-kx$만 고려하면 됩니다.

미방 수업에서 배우는 2차 homogeneous ODE를 푸는 방법으로 쉽게 풀 수 있습니다.

\[\lambda^2 + k \lambda = 0\]

특성방정식을 풀면 되는데, 허근이 나오는 경우입니다. 이때, 실근 없이 허수부만 존재합니다.

\[\lambda = \frac{-0 \pm \sqrt{0^2 - 4 k}}{2} = \pm \sqrt{-k} = \pm \sqrt{k} \cdot i\]

요 $\lambda$를 solution에 대입하고, 그것을 오일러 공식으로 지수함수로 변환하면…

\[x(t) = e^{\lambda t} = e^{\pm \sqrt{k} \cdot i} = \cos (\sqrt{k} t) \pm i \sin (\sqrt{k} t)\]

표현을 간단히 하기 위해 주기 $\omega$로 표현하겠다: $\omega = \sqrt{k}$.

요걸 실수부만 남겨서 정리하면… (2차 homo. ODE 정리한 포스트에서 많이 대충 넘어가는 중)

• $x_1(t) = \cos \omega t$
• $x_2(t) = \sin \omega t$

진동자는 무한히 주기 운동을 한다.

Damped Harmonic Oscillation

Simple 경우는 정말 간단하다. 여기서부터 조금 복잡해지는데, 그래도 미방의 다른 더 어려운 것들을 겪고 나면 이것도 좀 쉬워보인다 ㅋㅋ

\[x'' + bx' + kx = 0\]

이번에는 damping force인 $-bx’$가 추가되었다. 요거는 속도에 비례하는 힘으로, 공기(매질)에 대한 저항력이나 마찰력으로 해석한다.

요기서부터는 공식으로 답을 구할 때 항상 실수부가 존재한다.

\[\lambda = \frac{-b \pm \sqrt{b^2 - 4k}}{2}\]

그리고 $b^2 - 4k$가 양수, 음수, 중근인 경우로 나누는데…

---

[양수: $b^2 - 4k > 0$]

$x(t) = e^{\lambda t}$로 solution이 구해지는데, 이때 유의할 점이 $\lambda$가 항상 “음수“라는 것이다. 그 이유는 별거 없고 그냥 $b \ge \sqrt{b^2 - 4k}$이기 때문.

암튼 $e^{\lambda t}$에서 지수부가 음수이기 때문에, 항상 $t \rightarrow \infty$에서 0으로 수렴한다.

[중근: $b^2 - 4k > 0$]

요것 $\lambda = - b /2$가 되는데, 음수이기 때문에 함수가 0으로 수렴한다. 다만, 이 경우 solution 함수의 basis가 하나만 나오기 때문에, $t$텀을 붙여서 솔루션이 아래와 같이 나온다.

• $x_1(t) = e^{\frac{-b}{2}t}$
• $x_2(t) = t e^{\frac{-b}{2}t}$

[음수: $b^2 - 4k < 0$]

허근이 나오는데, Simple 케이스와 달리 실수부가 존재한다.

따라서, 식이 아래와 같이 계산되는데

\[x(t) = e^{-\frac{b}{2}t} \left( \cos \omega t \pm i \sin \omega t \right)\]

요것도 실수부만 남겨서 표현하면…

\[x(t) = e^{-\frac{b}{2}t} \left( C_1 \cos \omega t + C_2 \sin \omega t \right)\]

Damping 케이스에서 재밌게 본 부분은 그래프 모양에 있다.

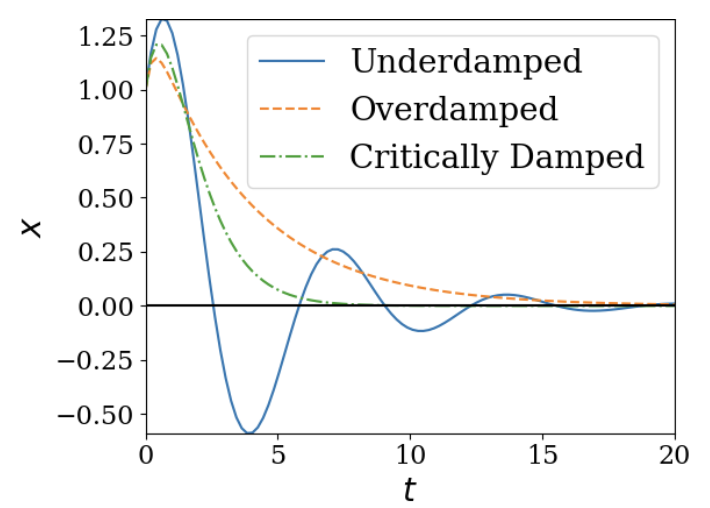http://www.physicsbootcamp.org

신기하게도 중근인 critically damped가 over damped 보다 빠르게 0에 수렴한다!! 그래프를 보면, 초기에는 critical damped의 값이 over damped 보다 커지는 경우도 존재한다!! 그럼에도 불구하고 더 빠르게 수렴하는 것!!

이런 현상이 생기는 이유는 over damped 상황에서는 댐핑이 너무 강해서 시스템 속도에 브레이크가 걸린 상태처럼 느리거 평형점에 다가가기 때문이라고 한다. 그래서 critical damped 케이스가 평형점에 가장 빠르게 접근하기 위한 조건이라고 한다.

문득 싸이클로이드의 예제가 생각이 났는데, 공이 가장 빠르게 가기 위해선 직선 거리보다는 운동거리가 더 길더라도 싸이클로이드 경로로 가야 한다는 예시가 떠올랐다. over vs. critical damped의 경우도 마찬가지로 빠르게 평형점에 도달하기 위해서는 저항이 너무 강해도 좋지 않은 것 같다. 과유불급(過猶不及)이라는 말이 있듯이 너무 지나치면 좋지 않은 것 같다.

Forced Harmonic Oscillation

사실 요 녀석이 내가 포스트를 쓰게 마음 먹게 한 녀석이다…;; 미방에서 언제나 머리 아프게 하는 것은 non-homogeneous 케이스인 것 같다.

\[x'' + bx' + kx = f(t)\]

조화 진동자에 외부힘 $f(t)$가 작용하는 경우이다. 그동안 살펴본 케이스들은 시스템이 $x$와 그들의 Derivative에만 의존하는 시스템이었는데, 여기서부터는 $f(t)$라는 시간 $t$에 대한 함수가 시스템에 추가된다. 그래서 “Non-autonomous” 시스템이 된다. 동시에 우변이 0이 아니라서 “Non-homogeneous”이기도 하다.

이때, $f(t)$가 그냥 임의의 함수가 아니라 주기성을 갖는 $f(t) = A \cos (\omega_f \, t)$라고 하자.

non-homogeneous ODE를 풀 때는

1. homo. ODE에서 얻어지는 general solution $x_h(t)$를 구하고
2. non-homo. ODE를 만족하는 어떤 구체적인 함수 $x_p(t)$를 구한 후
3. 둘을 일차 결합!!

해서 구했다. $x_h(t)$야 쉽게 구할 수 있고, $x_p(t)$를 구하는게 문제다.

Forced but Simple Harmonic Oscillation

$bx’$ 텀까지 고려하기엔 머리가 아프니까 일단 Simple인데 외부힘이 주어진 경우를 먼저 살펴보자.

\[x'' + kx = A \cos (\omega_f \, t)\]

[미정계수법]

particular solution이 sinusoidal 이므로 아래와 같은 particular solution 함수가 가능하다.

\[x_p(t) = a \cos (\omega_f \, t) + b \sin (\omega_f \, t)\]

요걸 좌변인 $x’’ + \omega^2 x$에 대입하면…

• $x’ = (-a \, \omega_f \, \sin (\omega_f \, t) + b \, \omega_f \, \cos (\omega_f \, t))$
• $x’’= (-a \, \omega_f^2 \, \cos (\omega_f \, t) - b \, \omega_f^2 \, \cos (\omega_f \, t))$

\[x'' + \omega^2 x = (\omega_f^2 - \omega) \cdot (a \cos (\omega_f \, t) + b \sin (\omega_f \, t))\]

그리고 LHS와 RHS가 같다고 가정하면…

• $(\omega_f^2 - \omega)a = A$
• $(\omega_f^2 - \omega)b = 0$

이 된다.

따라서, particular solution $x_p(t)$는 아래와 같고,

\[x_p(t) = \frac{A}{(\omega_f^2 - \omega)} \cos (\omega_f t)\]

이를 General solution으로 표현하면

\[x(t) = C_1 \cos (\omega \, t) + C_2 \sin (\omega \, t) + \frac{A}{(\omega_f^2 - \omega)} \cos (\omega_f t)\]

Envelope Oscillation

위의 forced but simple 케이스인데, $C_1$, $C_2$를 아래와 같이 설정한 경우이다.

• $C_1 = - \frac{A}{(\omega_f^2 - \omega)}$
• $C_2 = 0$

이렇게 하면, general solution은 아래와 같은데

\[x(t) = \frac{A}{(\omega_f^2 - \omega)} \left( \cos (\omega_f \, t) - \cos (\omega \, t) \right)\]

코싸인 함수의 덧셈은 아래의 공식을 따르므로…

\[\cos \alpha - \cos \beta = 2 \sin \left( \frac{\beta - \alpha}{2}\right) \sin \left( \frac{\beta + \alpha}{2}\right)\]

general solution을 아래와 같은 $\sin$, $\cos$의 곱셈으로 표현할 수 있다.

\[x(t) = \frac{A}{(\omega_f^2 - \omega)} \cdot 2 \sin \left( \frac{\omega - \omega_f}{2}\right) \sin \left( \frac{\omega + \omega_f}{2}\right)\]

이를 표기의 편의를 위해 $\delta = \frac{\omega - \omega_f}{2}$, $\bar{\omega} = \frac{\omega + \omega_f}{2}$라고 표기하겠다. $\delta$는 위상차를 의미한다고 볼 수 있다. $\bar{\omega}$는 평균 위상이라고 볼 수 있다.

만약, $\delta \lt \lt \bar{\omega}$라고 한다면, 아래와 같은 Envelope Oscillation이 발생한다. (“Beats”라고도 부른다.)

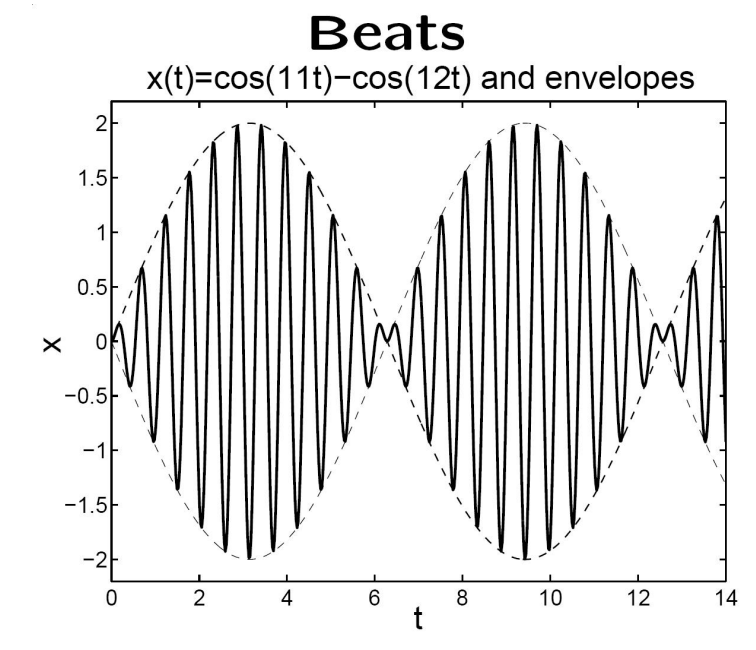University of Houston, Math 3331

작은 주기의 $\delta$는 느리게 변하는 진폭(envelop)를 그리고, 큰 주기의 $\bar{\omega}$는 빠른 진동으로 느린 진폭의 안을 채운다.

General Forced Harmonic Oscillation

\[x'' + bx' + kx = A \cos (\omega_f \, t)\]

다시 이 경우를 살펴보자. 위에서 Forced but Simple 케이스처럼 “미정계수법”을 이용해 particular solution을 구하면 된다. 구해보면… 아래와 같다.

\[x_p(t) = \frac{A}{\sqrt{(\omega^2 - \omega_f^2)^2 + 4 b^2 \omega_f^2}} \cos (\omega_f t - \phi)\]

되게 복잡하다;; 하지만 핵심은 particular solution이 주기 함수로 유도된다는 것이다. 이걸로 general solution을 만들어서 그래프를 살펴보면…

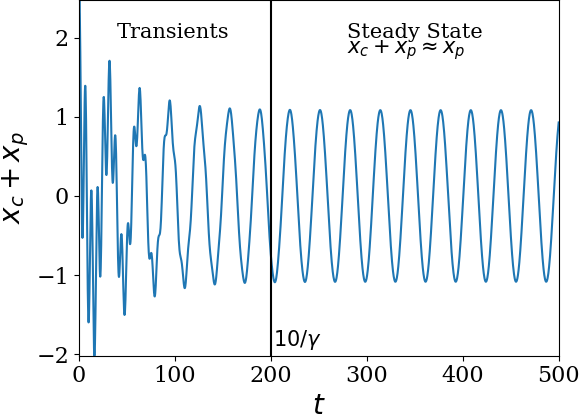http://www.physicsbootcamp.org

시스템이 초기에는 $x_h(t)$의 영향으로 불안정하지만(과도기; transient), $x_h(t) \rightarrow 0$으로 수렴하는 성질 때문에, 시간이 지나면 particular solution 그래프만 남게 된다.

References

• University of Houston, Math 3331
• http://www.physicsbootcamp.org - 1
• http://www.physicsbootcamp.org - 2