Saddle-Node Bifurcation

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

[Bifurcations]

• Saddle-Node Bifurcation 👋
• Pitchfork Bifurcation
• Hopf Bifurcation

Saddle-Node Bifurcation

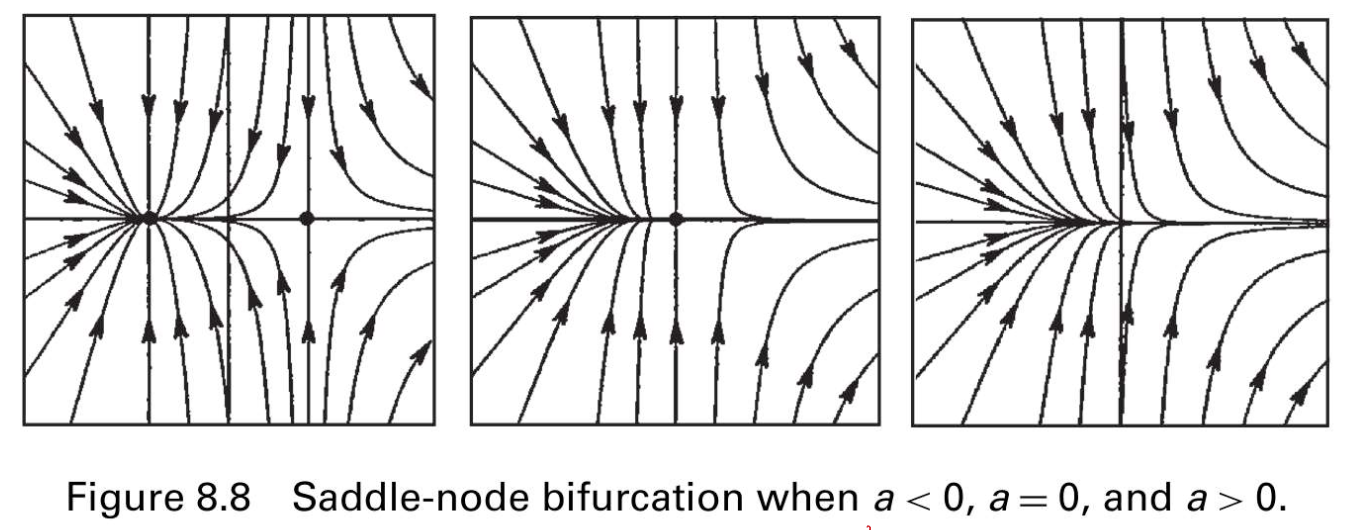
Linear System에서 Saddle Node의 Phase Portrait은 요렇게 생겼었다.

https://homepages.bluffton.edu/

우리는 이걸 Non-linear System에서도 Saddle-Node Bifurcation이 발생할 수 있음을 확인하고자 한다.

예제를 먼저 살펴보자.

1D Example

\[x' = a + x^2\]

이때, 그래프를 그려보면,

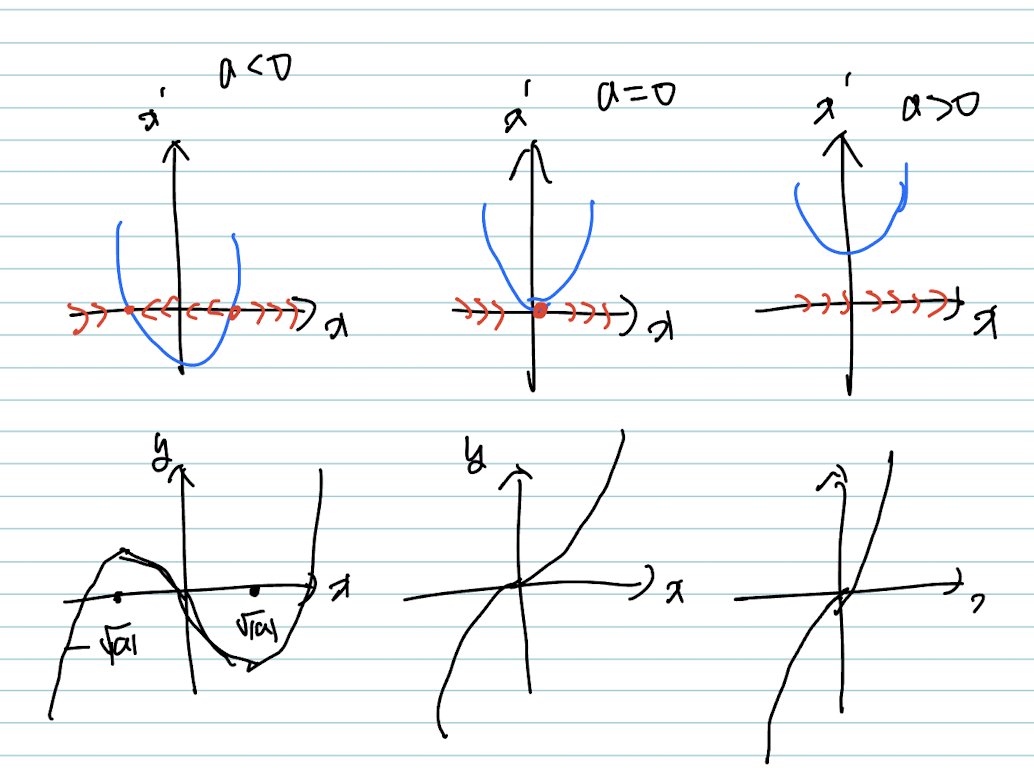
보면, parameter $a$ 값에 따라서, fixed point가 2개 -> 1개 -> 0개 순서로 달라집니다.

2D Example

\[\begin{aligned} x' &= a + x^2 \\ y' &= -y \end{aligned}\]

$x$에 대한 부분과 $y$에 대한 부분을 나눠서 생각하면 Phase Portrait을 그리기 쉬운 것 같다.

Definition

Saddle Node Bifurcation에 대해 엄밀 정의하면 아래와 같다.

There is an interval about bifurcation value $a_0$ and another interval $I$ on x-axis s.t.

$x’ = f_a(x)$ has

1. Two fixed points in $I$ if $a < a_0$ (or $a > a_0$)
2. One fixed point in $I$ if $a = a_0$
3. No fixed point in $I$ if $a > a_0$ (or $a < a_0$)

Saddle-Node Bifurcation Theorem

주어진 System이 Saddle-node bifurcation을 가진다면 공통적으로 만족하는 성질이 있다. 이를 기술한 것이 아래의 정리다.

$x’ = f_a(x)$ has a saddle-node bifurcation at $a = a_0$ when

1. $f_{a_0} (x_0) = 0$
2. $f_{a_0}’ (x_0) = 0$
3. $f_{a_0}’’ (x_0) \ne 0$
4. $\frac{\partial f_{a_0}}{\partial a} \ne 0$