Projection

복수전공하고 있는 수학과의 학부 졸업시험을 위해 2024년 10월부터 선형대수를 다시 공부하고 있습니다. (현재진행형… 🏃‍♂️‍➡️) 선형대수에 대한 전체 포스트 목록은 “Linear Algebra“에서 확인하실 수 있습니다!

들어가며

이 부분은 뭔가 고등학교 때 배운 “기하와 벡터”의 느낌이 조금 나는 것 같습니다 ㅋㅋ

그런데, 수능 이후로 고교 수학은 다시 펴본 적이 한번도 없어서 ㅋㅋ 배웠던 하나도 기억 안 나긴 한다… 😵‍💫

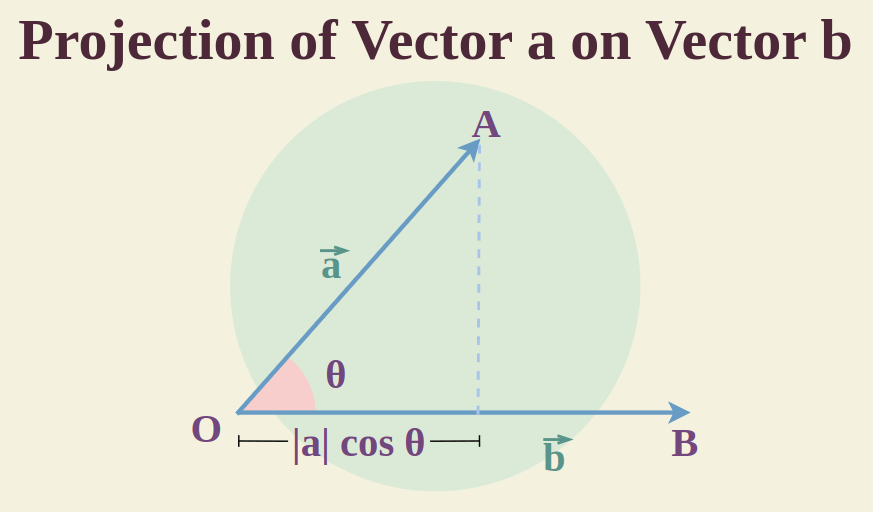
Projection on a vector

geeksforgeeks

어떤 벡터 $\mathbf{b}$를 다른 벡터 $\mathbf{a}$ 방향으로 변환하는 것 입니다. 표기는 아래와 같습니다.

\[\text{proj}_{\mathbf{a}}{\mathbf{b}} = \text{proj}_{\mathbf{a}}(\mathbf{b})\]

벡터 $\mathbf{b}$를 정사영한 것은 벡터 $\mathbf{a}$에 스칼라 배수 한 것과 같습니다. 따라서,

\[\text{proj}_{\mathbf{a}}(\mathbf{b}) = c \cdot \mathbf{a}\]

이때, 벡터 $\mathbf{a}$와 정사영 벡터 $c \cdot \mathbf{b}$를 빼주면, 이것은 정사영의 정의에 의해 축이 되는 벡터 $\mathbf{b}$와 수직하게 됩니다.

\[(\mathbf{b} - c \cdot \mathbf{a}) \cdot \mathbf{a} = 0\]

이제 식을 정리하면,

\[c = \frac{\mathbf{b} \cdot \mathbf{a}}{\vert \mathbf{a} \vert^2}\]

따라서, 정사영 벡터의 최종 형태는

\[\text{proj}_{\mathbf{a}}(\mathbf{b}) = \frac{\mathbf{b} \cdot \mathbf{a}}{\vert \mathbf{a} \vert^2} \cdot \mathbf{a}\]

Projection on a subspace

이번에는 벡터 $\mathbf{b}$를 평면(공간) $W$ 위에 정사영 해봅시다. 이것은 해당 평면(공간) $W$ 안에 있는 벡터 중 가장 벡터를 찾는 것과 같습니다. 표기는 아래와 같습니다.

\[\text{proj}_{W}{\mathbf{b}} = \text{proj}_{W}(\mathbf{b})\]

평면 위에 정사영하는 방법을 찾기 위해 평면이 어떻게 만들어지는지 찾아야 합니다. 보통은 행렬 $A$가 먼저 주어지고, 이것의 열벡터로 평면 $W$를 만들긴 하는데, 반대로 평면 $W$가 주어졌다면,

\[W = \text{span}(\mathbf{a}_1, \mathbf{a}_2, \dots, \mathbf{a}_k)\]

임을 이용해 행렬 $A \in \mathbf{R}^{n\times k}$를 만들어내면 됩니다.

이제 실제 정사영을 찾아봅시다! 가장 먼저, 벡터 $\mathbf{b}$를 $W$ 위로 정사영하면, 그 정사영된 벡터 $\mathbf{p}$는 평면 $W$에 속하게 되고 이것은

\[\text{proj}_{W}(\mathbf{b}) = \mathbf{p} \in W\]

그리고 정사영 벡터 $\mathbf{p}$는 열공간 $\text{Col}(A)$에 속하기도 합니다. 따라서, 정사영 벡터를 아래와 같이 표현할 수 있습니다.

\[\mathbf{p} = A \hat{\mathbf{x}}\]

이제, 오차 벡터를 정의 합니다.

\[\mathbf{e} = \mathbf{b} - \mathbf{p} = \mathbf{b} - A \hat{\mathbf{x}}\]

이 오차는 평면 $W = \text{Col}(A)$와 직교 해야 합니다. 따라서,

\[A^T \mathbf{e} = A^T (\mathbf{b} - A \hat{\mathbf{x}}) = \mathbf{0}\]

이제, 이 식을 잘 정리해서 $\hat{\mathbf{x}}$를 구하면,

\[\hat{\mathbf{x}} = (A^T A)^{-1} A^T \mathbf{b}\]

이제 처음에 정의 했던, 정사영 벡터 $\mathbf{p}$의 정의에 대입하면,

\[\text{proj}_{W}(\mathbf{b}) = A (A^T A)^{-1} A^T \mathbf{b}\]

Projection Matrix

위에서 수행한 평면으로의 정사영 $\text{proj}_W(\mathbf{b})$를 수행해주는 함수 같은 행렬을 정의할 수 있습니다. 이를 “정사영 행렬“이라고 합니다.

행렬 자체는 그냥 위에서 유도한 정사영 공식에서 가져오면 됩니다.

\[P = A (A^T A)^{-1} A^T\]

이 정사영 행렬은 몇가지 특징이 있는데요!

• 대칭성
  • 정사영은 대칭 연산이기 때문에, 행렬도 이를 반영 합니다.
  • $P^T = P$
• 멱등성
  • 정사영을 2번 이상 진행해도, 처음 사영한 결과에서 바뀌지 않습니다.
  • 따라서, $P^n = P^2 = P$