Demand Functions

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

Budget Sets

“예산 집합”은 주어진 예산 $w$와 각 재화에 대한 고정된 가격 $p_1$, $p_2$가 있을 때 각 재화를 구매할 수 있는 가능한 번들을 모두 모은 집합 입니다.

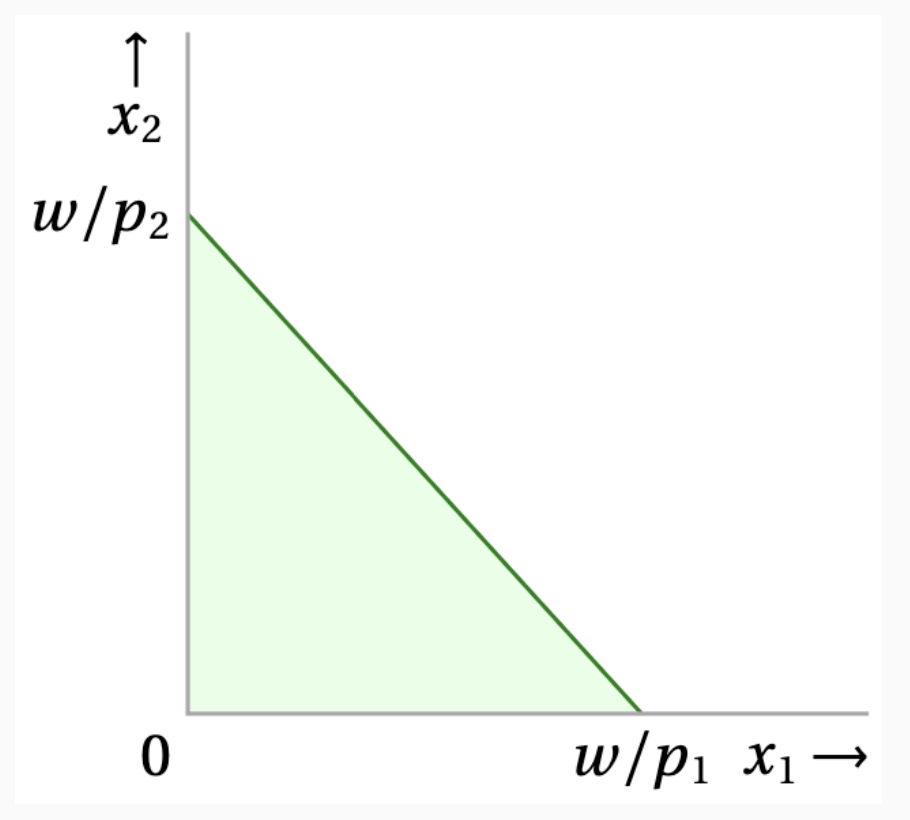
표기는 아래와 같습니다.

\[B((p_1, p_2), w) = \left\{ (x_1, x_2) \in X : p_1 x_1 + p_2 x_2 \le w \right\}\]

이때, 예산을 한계치까지 사용하는 번들의 집합을 “Budget Line“이라고 합니다.

\[\left\{ (x_1, x_2) \in X : p_1 x_1 + p_2 x_2 \; {\color{red} =} \; w \right\}\]

집합이 “볼록(convex)“하다는 것은 내부의 어떤 두 점을 잡더라도, 그 사이을 있는 선분 위의 모든 점이 그 집합에 다시 속한다는 것을 말합니다. 모든 budget set은 볼록 성질을 갖습니다.

이것은 두 점 $x, y$가 예산 조건을 만족하는 소비 였다면, 선형 조합(Linear Combination)한 새로운 소비 선택 $z = \lambda x + (1-\lambda) y$도 여전히 예산을 만족한다는 것을 말합니다.

고정 수익이 있다면, 예산 집합이 사다리꼴 모양이 될 수도 있음!!

단순히 직선이 아니라 다양한 형태의 예산 집합이 존재할 수 있음.

Exchange Economy

“교환 경제”에서 사람들은 오직 물물 교환으로 원하는 것을 얻어야 합니다. 그리고 “돈”이라는 개념도 없습니다!

이런 경제 환경에서 각 소비자는 본인의 초기 재화 $e = (e_1, e_2)$를 가지고 있습니다. 그리고 이 재화를 시장에서 교환비에 따라 교환할 수 있습니다.

재화1 하나를 재화2 $\beta>0$개로 바꿀 수 있다면, 소비자가 가질 수 있는 번들 집합을 아래와 같이 적을 수 있습니다. 이때, $x = (x_1, x_2)$는 교환 갖게 되는 번들 입니다. 재화1을 교환하는 상황이기 때문에, 가장 먼저 아래의 부등식이 성립합니다.

\[x_1 \le e_1 \quad \text{and} \quad x_2 \ge e_2\]

• 재화1은 기존 보유량보다 줄어듭니다 $x_1 \le e_1$
• 재화2는 교환으로 인해 보유량이 늘어납니다 $x_2 \ge e_2$

그리고 교환비 $\beta$를 고려해 식을 만들면 아래와 같습니다.

\[\left\{ (x_1, x_2) \in X : (x_2 - e_2) = (e_1 - x_1) \beta \right\}\]

• 좌변
  • $(x_2 - e_2)$는 교환으로 얻은 재화2의 수량 입니다.
• 우변
  • $(e_1 - x_1)$는 시장에 내놓은 재화1의 수량 입니다.
  • 시장의 교환비 $\beta$에 따라서, 얻을 수 있는 재화2의 수량은 $(e_1 - x_1)\beta$가 됩니다.

이때 소비자는 교환비 $\beta > 0$로 하지 않고, 교환비보다 적은 수량 만큼 재화2를 수령할 수도 있습니다. (저렴하게 교환 받는 거는 자유니까요!) 단, 시장의 교환비 $\beta$보다 많은 수량을 교환 받을 수는 없습니다!

그래서 예산 집합은 아래와 같이 부등식의 형태가 됩니다.

\[\left\{ (x_1, x_2) \in X : (x_2 - e_2) \; {\color{red} \le} \; (e_1 - x_1) \beta \right\}\]

이 부등식을 잘 정리하면 예산 집합을 얻을 수 있습니다.

\[\left\{ (x_1, x_2) \in X : \beta x_1 + x_2 \le \beta e_1 + e_2 \right\}\]

우변의 $\beta e_1 + e_2$는 고정값 입니다. 이걸 예산 $w$라고 봅니다. 좌변은 예산 안에서 내가 가질 수 있는 재화의 조합을 의미 합니다: $B((\beta, 1), \beta e_1 + e_2)$.

표기를 재화의 가격을 기준으로 아래와 같이 할 수도 있습니다.

\[B((p_1, p_2), w) = \left\{ (x_1, x_2) : p_1 x_1 + p_2 x_2 \le w \right\}\]

교환비 $\beta$ 대신에, 각 재화의 가격 $p_i$로 표현 합니다!

Demand Function

“수요 함수”는 각 예산 집합 $B((p_1, p_2), w)$ 안에서 소비자 선택한/선택할 번들을 매핑하는 함수 입니다.

\[x : B \rightarrow (x_1^{\ast}, x_2^{\ast})\]

$B((p_1, p_2), w)$는 소비자가 주어진 예산 $w$ 안에서 선택 가능한 모든 번들의 집합입니다. $x((p_1, p_2), w) = x(B)$는 소비자가 예산 집합 내에서 선택한 번들 입니다. 이때, 소비자는 자신의 효용(utility)가 극대화 되는 최적의 소비 번들을 선택 합니다.

또, 소비자는 예산을 최대한 사용하도록 소비를 합니다! 이것은 최적의 소비가 항상 “Budget Line” 위에서 일어난다는 것을 말합니다.

Examples

Equal Amounts of the Goods

소비자는 두 상품의 항상 같은 갯수가 되도록 구매 합니다. 즉, 예산 집합 안에서 $x_1 = x_2$가 되고, 그 갯수가 최대가 되는 소비를 합니다. 그러면, 수요 함수의 결과는 아래와 같습니다.

\[p_1 x_1 + p_2 x_2 = (p_1 + p_2) x^\ast = w\]

따라서,

\[x(B) = (x^{\ast}, x^{\ast}) = \left(\frac{w}{p_1+p_2}, \frac{w}{p_1+p_2}\right)\]

Half Spent on each Good

이번에는 재화의 절반씩을 각 상품에 소비하는 소비자 입니다. 이 경우 수요 함수의 결과는 아래와 같습니다.

\[\begin{aligned} p_1 x_1^{\ast} &= w / 2 \\ p_2 x_2^{\ast} &= w / 2 \\ \end{aligned}\]

따라서,

\[x(B) = (x_1^{\ast}, x_2^{\ast}) = \left(\frac{w}{2p_1}, \frac{w}{2p_2}\right)\]

실제로 이런 소비자들이 있을 것 같고, 지금까지의 예시 수요 함수들도 별도 어렵지 않습니다 ㅎㅎ

All Wealth Spent on the Cheaper Good

이 소비자는 두 상품 중 가격이 더 저렴한 상품만을 모조리 구매하려는 소비 성향을 가지고 있습니다. 그래서 수요 함수의 결과가 이렇게 나옵니다.

\[x(B) = \begin{cases} \left(\dfrac{w}{p_1}, 0\right) & \text{if} \; p_1 < p_2 \\ \left(\dfrac{w}{2p_1}, \dfrac{w}{2p_2}\right) & \text{if} \; p_1 = p_2 \\ \left(0, \dfrac{w}{p_2}\right) & \text{if} \; p_1 > p_2 \end{cases}\]

Purchase one good up to limit

이 소비자는 상품 $x_1$을 어떤 한계치(ex: 7개)까지 구매하는 것을 우선시 합니다. 상품 $x_1$에 대한 구매가 충족되면, 이후부터는 남은 금액으로 $x_2$를 구매 합니다.

\[x(B) = \begin{cases} \left(\dfrac{w}{p_1}, 0\right) & \text{if} \; w/p_1 \le 7 \\ \left(7, \dfrac{w-7p_1}{p_2}\right) & \text{otherwise} \end{cases}\]

맺음말

이어서 “소비자 문제(Consumer’s Problem)”에 대해 살펴봅니다! 여기에서 살펴본 예산 집합(Budget Set)과 수요 함수(Demand Function)를 종합하는 내용 입니다!

➡️ Consumer’s Problem