Rationalizable Demand Function

졸업을 위해 마지막 학기에 “미시경제학” 수업을 듣게 되었습니다. 경제학원론 수업을 재밌게 들어서 경제 쪽이랑 궁합이 좋은 줄 알고 신청 했는데, 웬걸… 이 과목은 사실상 수학과 과목 이었습니다.. ㅋㅋ 그래도 수학과 복수전공도 하고 있으니, 이 수업도 힘내서 잘 들어봅시다! 전체 포스트는 “미시경제학” 카테고리에서 확인하실 수 있습니다.

들어가며

수요 함수 $x(B)$가 출력하는 결과가, 실제로 선호의 극대화를 만족한다면, 그 수요 함수는 항상 최적 선택을 하도록 하는 “아주 좋은 함수” 일 겁니다!

A demand function is “rationalizable”,

if there is a ‘monotone’ preference relation s.t.

for every budget set the result of demand function is a solution of the consumer’s problem.

그래서, 어떤 수요 함수 $x(B)$가 주어 졌을 때, “이게 정말 소비자 선호를 극대화 해주는 선택인지?” 검증하거나 그 조건을 살펴보도록 하겠습니다.

(review) Rationalizable Choice Function

미시경제학 수업을 듣는 초반에, 선택 함수의 합리성에 대해 배웠습니다. 이번에도 ‘합리성’에 대해 다루길래 생각이 나서 가져와봤습니다 ㅎㅎ

합리적인 선택 함수는 소비자가 고른 결과에 “일관성“이 있어야 했습니다. 그리고 이 일관성은 소비자의 선호가 나이스한 조건을 만족해야 했습니다. 그리고 Property $\alpha$라는 성질을 만족한다면, 바로 그 선택 함수의 일관성이 확보되었습니다!

마찬가지로 합리적인 수요 함수는, 그 결과가 소비자에게 최대 효용을 주는 번들을 출력하도록 할 겁니다!

How to Check Rationality

수요 함수가 “합리적”이기 위해선 아래 조건을 만족해야 합니다.

• 예산 조건
  • 솔루션은 항상 예산 조건 $p \cdot x = w$ 위에 존재해야 합니다.
• 단조성
  • 예산 집한 내에서 가장 효용이 큰 번들이어야 합니다.
• 선택 일관성
  • 동일 조건이 다시 주어졌을 때, 선택이 변하지 않아야 합니다.
  • 이것은 이후에 “현시선호 일관성(WARP)“라는 성질이라고 부릅니다!
• 선호 가능성
  • 어떤 효용 함수로 이 수요를 설명할 수 있어야 합니다.

하나 헷갈렸던 건, 처음에 수요 함수에 대해 살펴봤을 때, 해의 존재성 조건으로 아래 3가지 조건이 있었습니다.

• Continuous
• Strictly Convex
• Monotone

“해의 존재성”은 소비자 문제가 풀리는(solvable) 문제인지 판단하는 기준 입니다.
반면에, “합리성”은 소비자 문제의 해가 의미 있는 솔루션인지 판단하는 기준 입니다.

그래서 해는 존재하지만, 합리성은 없는 그럼 수요 함수도 존재 합니다! 아래의 예시에서 “가격에 상관 없이 더 비싼 재화”를 선택하는 경우가 바로 그 녀석 입니다 ㅎㅎ

Examples

All spent on the Cheaper Goods

두 재화가 있을 때,

• 두 재화의 가격이 다르면, 가격이 저렴한 것에 모든 예산을 사용하고,
• 두 재화의 가격이 같으면, 각각에 절반씩 예산을 사용하는

수요 함수가 있다고 하자. 이 수요 함수는 합리적인가?

정답은 합리적인 수요 함수 입니다! (헐!) 이 수요 함수는 $x_1 + x_2$라는 선호를 가진 것으로 표현할 수 있습니다. 또, 이런 수요 함수는 $\max(x_1, x_2)$라는 선호로 합리성을 표현할 수 있습니다.

Half spent on each

이번에는 가격에 상관 없이 두 재화에 각각 절반씩 예산을 사용하는 수요 함수가 있습니다.

이 수요 함수도 합리적인 수요 함수인데, 왜냐하면 선호를 $u(x) = x_1 x_2$라는 효용 함수로 표현할 수 있기 때문입니다.

All spend on the expensive Goods

이번에는 가격에 상관 없이 더 비싼 재화에 모든 재화를 사용하는 경우 입니다.

그런데, 이 경우는 합리적인 수요 함수로 표현할 수 없습니다! 반례가 있는데요!

소비자가

• $B((1, 2), 2)$라는 예산에서는 $a = (0, 1)$를 선택 했고,
• $B((2, 1), 2)$라는 예산에서는 $b = (1, 0)$를 선택 했습니다.

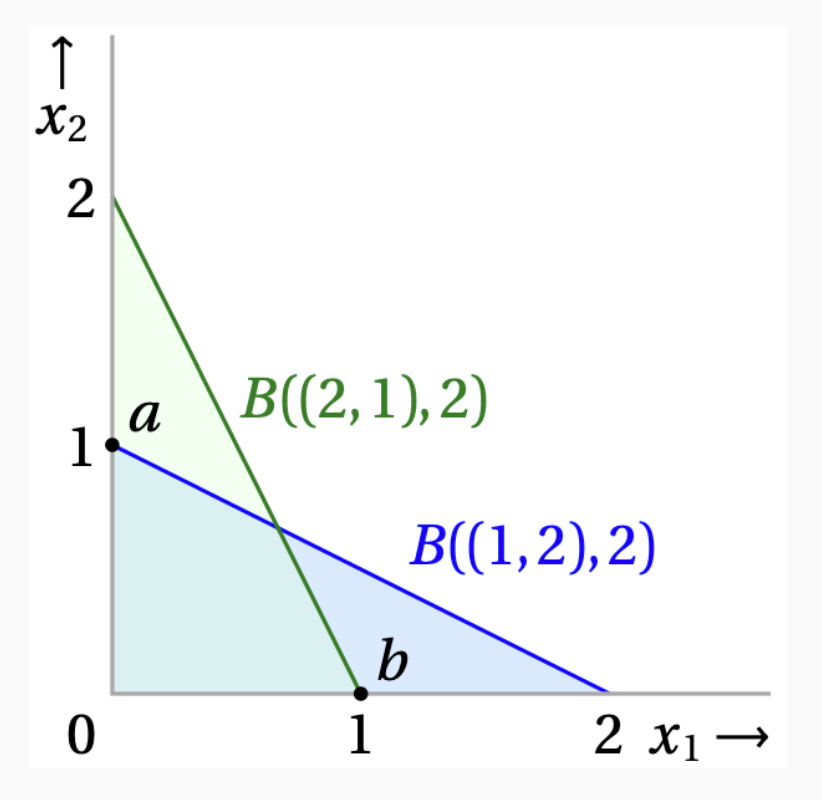
소비자의 이런 경향은 “단조성”을 위배 합니다.

$B((1, 2), 2)$라는 예산 집합에서 $b = (1, 0)$은 예산 집합 내부에 있으므로, 단조적 선호를 따른다면, 선택 될 수 없습니다.
(단조성에 따르면, 내부보다는 경계나 예산 밖의 것이 더 선호 됩니다.)

이것은 $B((2, 1), 2)$에서도 동일하게 발생합니다. 단조성을 만족하지 않고 내부의 번들이 경계/외부의 번들보다 더 선호되는 현상이 발생합니다.

이것은 선호의 단조성을 위배한다는 것이고, 이런 수요 함수는 “비합리적인” 결정을 내린다고 판단 합니다.

맺음말

이어서 소비자가 어떻게 행동하는지에 따라 재화를 분류하는 것에 대해 살펴봅니다!

➡️ Kind of Goods

• Derived Functions
  • Regular Demand Function
  • Cross Demand Function
  • Engel Function
• Normal Goods
• Regular Goods
• Inferior Goods
• Giffen Goods