Bayes’ Rule
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Law of Total Probability
Definition. Partition
The events $\{ B_1, \dots, B_n \}$ form a partition of event space $S$ if
- $B_i \cap B_j = \emptyset$ for any $i \ne j$
- $\cup^n_{i=1} B_i = S$
Theorem. Law of Total Probability
If the events $B_1$, …, $B_n$ form a partition of $S$ such that $P(B_i) > 0$,
then for any event $A$
\[P(A) = \sum^{n}_{i=1} P(A \cap B_i)\]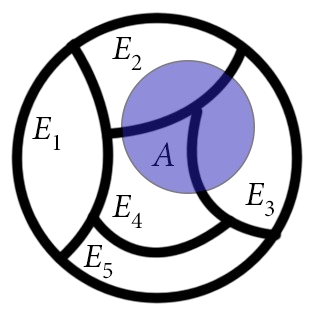
<전체 확률의 법칙; Law of Total Probability>는 <Rule of Elimination>라고도 한다.
Bayes’ Rule
Theorem. Bayes’ Rule
If the events $B_1$, $B_2$, …, $B_k$ be a partition of event space $S$,
then for any event $A$ with $P(A) > 0$
\[P(B_k \mid A) = \frac{P(B_k \cap A)}{P(A)} = \frac{P(A \mid B_k)P(B_k)}{\sum^{n}_{i=1} P(A \mid B_i)P(B_i)}\]proof.
증명은 간단하다.
[Step 1] Conditional Probability에 따라 아래의 식이 성립한다.
\[P(B_k \cap A) = P(B_k \mid A) P(A) = P(A \mid B_k) P(B_k)\]식을 약간 다음으면 아래를 유도할 수 있다.
\[P(B_k \mid A) = \frac{P(B_k \cap A)}{P(A)}\][Step 2] Law of Total Probability에 따라 분모의 $P(A)$를 아래와 같이 바꿀 수 있다.
\[\frac{P(B_k \cap A)}{P(A)} = \frac{P(B_k \cap A)}{\sum^{n}_{i=1} P(A \cap B_i)}\][Step 3] 다시 Conditional Probability의 정의를 이용하면, 최종적으로 아래의 결과를 얻는다.
\[\frac{P(B_k \cap A)}{\sum^{n}_{i=1} P(A \cap B_i)} = \frac{P(B_k \cap A)}{\sum^{n}_{i=1} P(A \mid B_i)P(B_i)}\]Applications of Bayes Rule
<Bayes Rule> 자체는 어렵지 않다. 그러나 <Bayes Rule>은 예제와 언제/어떻게 이걸 써야 하는지를 확실히 아는게 중요하다. 👏
선별 검사
건강한 사람과 특정 질병이 있는 사람을 구별하기 위해 시행하는 검사를 <선별 검사; Screening Test>라고 한다. 선별 검사에서 이상이 나타나면, 정밀 검사를 통해 질병의 유무를 판단한다.
건강한 블혼은 아침부터 목이 아프기 시작했다. 혹시 코로나에 걸렸나 싶어서 아침에 자가검사키트를 사서 해봤더니 이럴수가! 양성(+)이 떴다!
2022년 대한민국에서 코로나 걸릴 확률 $P(C)$는 $0.4$라고 하자. 그리고 자가검사키트의 정확도는 (1) 코로나에 걸린 사람이 양성일 확률 $P(+ \mid C)$은 $0.95$, (2) 코로나에 걸리지 않은 사람이 양성일 확률 $P(+ \mid \sim C)$은 $0.01$라고 하자.
블혼은 ‘사실 코로나에 걸리지 않은 건데 양성이 뜬 것일 수도 있다’고 생각하며’ 자가검사키트의 정확도를 의심하고 있다. 블혼을 위해 자가검사 양성인데 코로나에 걸렸을 확률 $P(C \mid +)$를 구해보자.
By Bayes’ Rule,
\[\begin{aligned} P(C \mid +) &= \frac{P(+ \mid C) P(C)}{P(+)} = \frac{P(+ \mid C) P(C)}{P(+ \mid C)P(C) + P(+ \mid \sim C)P(\sim C)} \\ &= \frac{0.95 \cdot 0.4}{0.95 \cdot 0.4 + 0.01 \cdot 0.6} = \frac{0.38}{0.386} \\ &= 0.98 \end{aligned}\]아… 아쉽지만, 자가검사기트에서 양성이 나왔다면, 블혼은 정말로 코로나에 걸렸을 확률이 무지무지 높은 것이다!!
Meaning of Bayes Rule
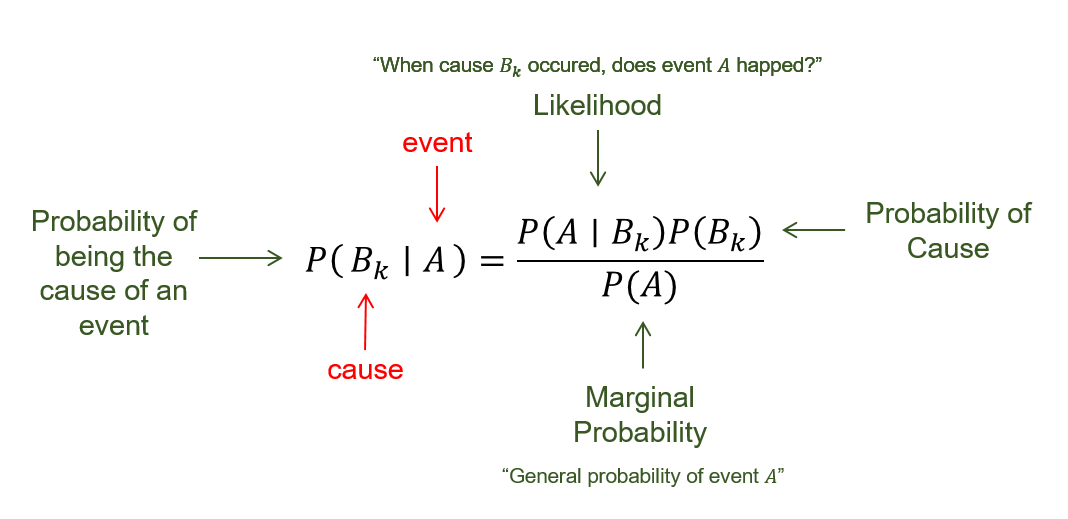
베이즈 정리는 이벤트에 대한 원인을 규명하는 도구이다. 어떤 이벤트가 일어나는 것에는 원인이 있다. 이 원인들은 2개가 동시에 발생하지는 않는 Exclusive 하다고 가정한다.
베이즈 정리를 관측(evidence)에 따른 믿음(belief)의 변화로 이해한 것이 <Bayesian; 베이즈 주의자>들이다.
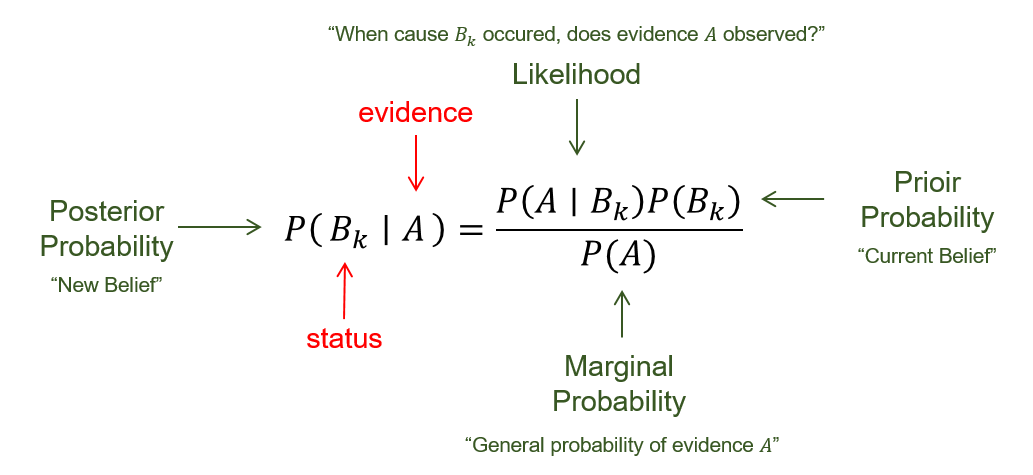
앞에서 살펴본 “코로나에 걸린 블혼”의 예시를 다시 보자. 그는 키트로 양성(+) 판정을 받기 전에는 자신의 감기가 코로나일 거라는 믿음이 $P(C) = 0.4$에 불과 했다. 그러나 키트로 양성 판정을 받은 후에는 자신이 코로나에 걸렸을 거라는 믿음 $P(C \mid +)$이 $0.98$로 치솟았다!
<베이즈 주의자>라는 게 사실은 그리 대단한 존재들이 아니다. 관찰된 사실을 바탕으로 본인의 믿을을 갱신하는 사람이라면 모두가 <베이즈 주의자>이다! 베이즈 주의자 만세!
맺음말
이번에 살펴본 <베이즈 규칙>은 <베이즈 통계학; Bayesian Statistics>라는 통계학 분야의 첫 걸음이다. “믿음에 자료를 반영해 믿음을 갱신한다”는 아이디어에 관심이 있다면, 베이지안을 공부해보자!
아쉽지만 학교에서 들은 “확률과 통계(MATH230)”에서 베이지안이 등장하는 건 <Bayes’ Rule> 뿐이다. 이것만 알고 까먹으면 된다 오히려 머신러닝이나 인공지능 수업에서 베이지안에 대한 이론을 더 공부한 것 같다. 혼종 수학자가 되어보자!!
<Bayes’ Rule>을 활용한 재밌는 문제가 있다! <몬티 홀 문제; Monti Hall Problem>이라는 문제가 있다. 더 말하면 스포가 될 것 같으니 궁금하다면 한번 도전해보자!