Probability and Statistics

2021-1학기에 수강한 POSTECH 김건우 교수님의 “확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 지킬 블로그입니다. 현실을 적당한 확률 분포로 모델링 하고, 또 확률을 기반으로 검정을 진행해 의사 결정을 수행하는 접근법을 배울 수 있었습니다 😁

---

Probability Theory

• Sample Space
  • Sample Space & Event
  • Permutation & Combination
• Probability of an Event
  • Probability
  • Conditional Probability
    • Independent Events
• Bayes’ Rule
  • Law of Total Probability
  • Meaning of Bayes Rule
• Monti Hall Problem¹

• Random Variables and Probability Distributionss
  • Random Variable $X$
  • Probability Distributions
    • PMF $f(x)$ & CDF $F(x)$ for Discrete RV
    • PDF $f(x)$ & CDF $F(x)$ for Continuous RV
• Joint Probability Distribution
• Mean, Variance and Covariance
• Chebyshev’s Inequality

• Discrete Probability Distribution - 1
  • (Discrete) Uniform Distribution
  • Bernoulli Distribution
  • Binomial Distribution
    • Multinomial Distribution
• Discrete Probability Distribution - 2
  • HyperGeometric Distribution
    • Multivariate HyperGeometric Distribution
  • Geometric Distribution
    • Negative Binomial Distribution
      • Negative Binomial Theorem 🎈
• Poisson Distribution
  • Law of Rare Events
  • Bernoulli Process & Poisson Process

• Continuous Probability Distribution
  • Uniform Distribution
  • Normal Distribution
  • Exponential Distribution
  • Gamma Distribution
  • Chi-square Distribution
  • Beta Distribution
  • Log-normal Distribution
  • Weibull Distribution (optional)

• Transformations of Random Variable - 1
• Transformations of Random Variable - 2
• Momemtum Generating Function

---

Statistics

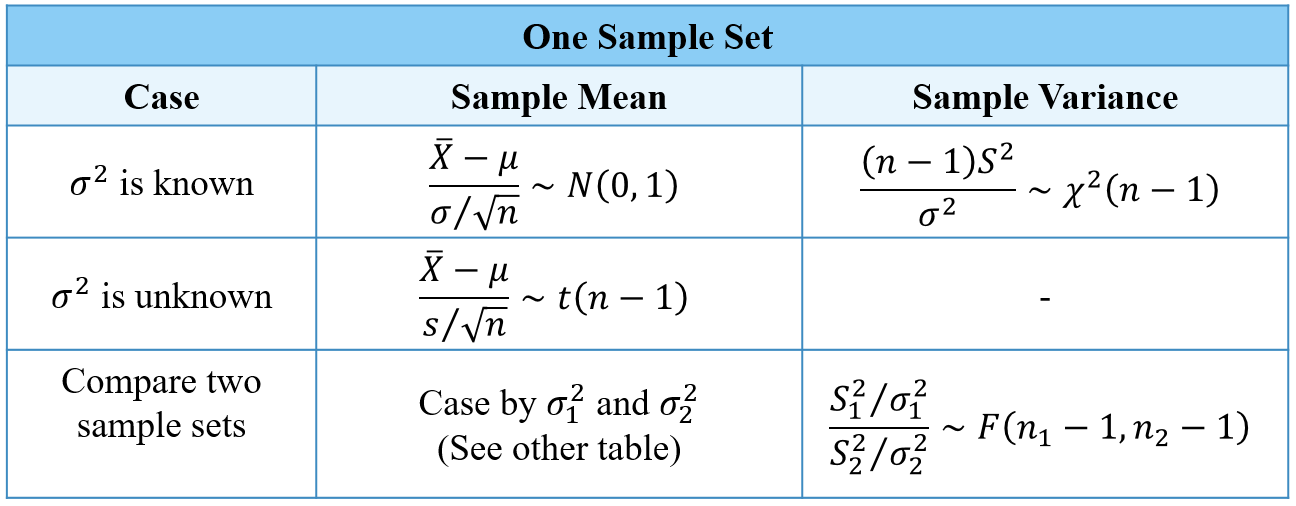
• Sampling Distribution
  • statistic; 통계량
    • sample distribution
• Sampling Distribution of Mean
  • WLLN; Weak Law of Large Numbers
  • CLT; Central Limit Theorem
    • proof
• Sampling Distribution of Variance
• Student’s t-distribution
  • Population Variance $\sigma^2$ is unknown
• F-distribution
• EDF and Quantile

• Point Estimation
  • unbiased estimator: $E(\hat{\Theta}) = \theta$
  • variance of estimator: $\text{Var}(\hat{\Theta})$
  • the most efficient estimator
  • Mean Squared Error of estimator
• Interval Estimation
  • z-value: Estimate $\mu$ when $\sigma^2$ is known
  • t-value: Estimate $\mu$ when $\sigma^2$ is unknown
• Prediction & Tolerance Estimation
• Two Samples Estimation: Diff Btw Two Means
• Two Samples Estimation: Paired Observations
• Proportion Estimation
  • Single Sample Estimation: Proportion Estimation
  • Two Samples Estimation: Diff Btw Two Proportions
• Variance Estimation
  • Single Sample Estimation: Variance Estimation
  • Two Samples Estimation: The ratio of two variances
• Maximum Likelihood Estimation

• Introduction to Hypothesis Tests
  • Null Hypothetsis $H_0$ & Alternative Hypothesis $H_1$
  • Test Statistic
    • Rejection Region or Critical Region; $X \ge C$
    • Critical Value; $C$
  • Type 1 Error & Type 2 Error
    • Significance level; Size of Test; 유의 수준 $\alpha$ 🔥
    • Power of Test; 검정력 $\gamma(\theta)$ 🔥
    • p-value; 유의 확률 🔥🔥
• Sample Mean Test
• Choice of Sample Size for Testing Mean
• Proportion Test
• Variance Test
• Chi-square Goodness-of-fit Test
  • Chi-square-Test; 카이제곱-검정
  • Test on Independence
  • Test on Homogeneity

• Introduction to Linear Regression
  • Simple Linear Regression
  • Least Square Method
    • unbiased regression coefficients
  • R-square $R^2$; 결정 계수
• Test on Regression
  • Distribution of Regression Coefficients $B_0$ and $B_1$
  • Estimator of $\sigma^2$
• Prediction on Regression
  • Estimate on Mean Response $\mu_{Y \mid x_0}$
  • Prediction Interval

---

Problem Solving

Probability

(준비중입니다! 😉)

Statistics

• PS1
  • sample variance $S^2$ is not the minimal variance estimator
  • MSE(Mean Squared Error) is sum of variance and square of bias
  • Compare $S^2$ and $\hat{S}^2$ using MSE
• PS2
  • $\sum e_i = 0$
  • $\sum x_i e_i = 0$
  • $\text{SST} = \text{SSR} + \text{SSE}$
• PS3
  • Variance of estimator $B_0$
  • unbiased estimator of $\sigma^2$ is $s^2$
  • (not yet) $s^2 \perp B_1$, and $s^2 \perp B_0$
  • (not yet) the distribution of $s^2$

---

Eassays

• Degree of Freedom in Statistics

---

Study Materials

• 『Probability & Statistics for Engineers & Scientists』 Walpole·Myers·Myers·Ye, 9th ed.

---

1. 정규수업 내용은 아니지만, 교수님께서 수업 시간에 잠깐 언급하셨습니다 😊 ↩