Random Variables and Probability Distributions
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Random Variable
Definition. Random Variable
A <random variable> is a function from $S$ to $\mathbb{R}$ s.t.
\[X: S \longmapsto \mathbb{R}\]Random Variable을 표현하는 규칙으로는
- Random Variable은 대문자로 표기한다. $X$, $Y$, $Z$
- 소문자 $x$는 Random Variable이 가질 수 있는 값(= 치역의 값) 중 하나를 의미한다.
만약 Random Variable $X$가 0, 1 둘 중 하나를 택하는 것과 같이 두 값 중 하나를 취하는 function이라면, 이것을 <Bernoulli Random Variable>이라고 한다.
Discrete vs. Continuous
Definition. Discrete Sample Space
If a sample space $S$ contains a finite or an unending sequence of possibilities, it is called a <discrete sample space>.
Definition. Continuous Sample Space
If a sample space $S$ contains an infinite number of possibilities or equal to the number of points on a line segment, it is called a <continuous sample space>.
즉, Sample Space $S$의 Cardinality에 따라 “Discrete”이냐 “Continuous”가 나뉜다.
Definition. Discrete Random Variable
A random variable is called a <discrete random variable>, if its set of possible outcomes it countable.
Definition. Continuous Random Variable
A random variable is called a <continuous random variable>, if its set of possible outcomes it uncountable.
즉, Random Variable의 치역의 Cardinality에 따라 “Discrete”이냐 “Continuous”가 나뉜다.
Probability Distribution
Discrete Prability Distribution
A discrete random variable assumes each of its values with a certain probability.
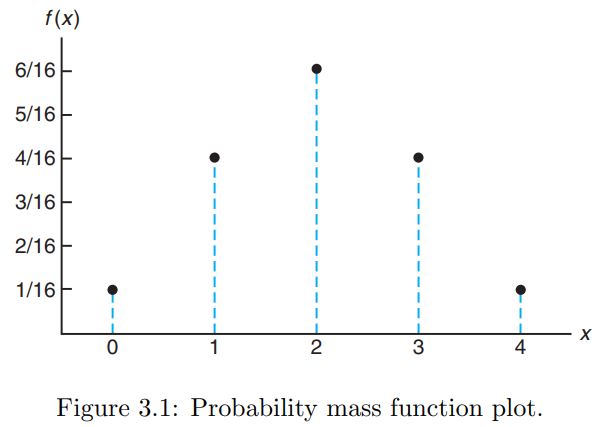
정리하면, Discrete RV $X$가 가질 수 있는 어떤 값 $x$에 대해, 그것에 대응되는 확률 $P(X = x)$가 어떤 값으로 정해진다는 말임. 그리고 이걸 $f(x)$의 형태로 표현한 것이 바로 <Probability Distribution>임.
Definition. Probability Mass Function; Probability Distribution
The set of ordered pairs $(x, f(x))$ is a <probability function>, <probability mass function>, or <probability distribution> of the discrete RV $X$, if for each possible outcome $x$,
- \[f(x) \ge 0\]
- \[\sum_x f(x) = 1\]
- \[P(X = x) = f(x)\]
위와 같은 probability function $f(x)$는 RV $X$가 $x$에서 갖는 <확률 probability>을 출력해준다.
Definition. Cumulative Distribution Function for Discrete RV
The <cumulative distribution function> $F(x)$ of a discrete RV $X$ with probability distribution $f(x)$ is
\[F(x) = P(X \le x) = \sum_{t \le x} f(t), \quad \mbox{for} - \infty < x < \infty\]개인적으로 PMF에 $\sum$을 한거라 명칭이 CMF가 되야 하지 않나 싶었는데, 교재에 “CMF”란 용어는 존재하지 않았다. 즉, <Cumulative Distribution Function>, 이게 맞는 표현이다.
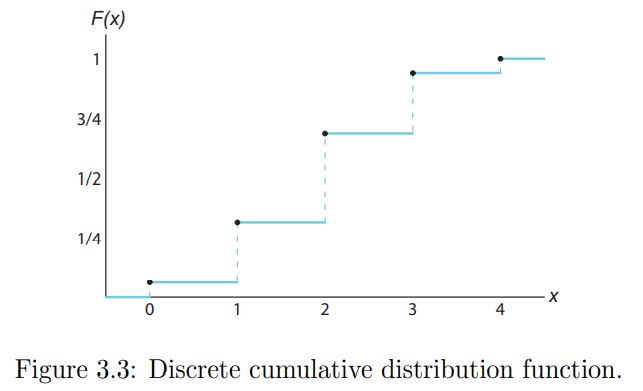
앞의 내용을 미리 스포하자면, <Discrete RV>와 <Continuous RV>에서의 CDF는 다르게 표현된다.
1. CDF $F(x)$ of a discrete RV $X$ with probability distribution $f(x)$
\[F(x) = P(X \le x) = \sum_{t \le x} f(t)\]2. CDF $F(x)$ of a continuous RV $X$ with density function $f(x)$
\[F(x) = P(X \le x) = \int^{x}_{-\infty} f(t) \; dt\]Continuous Prability Distribution
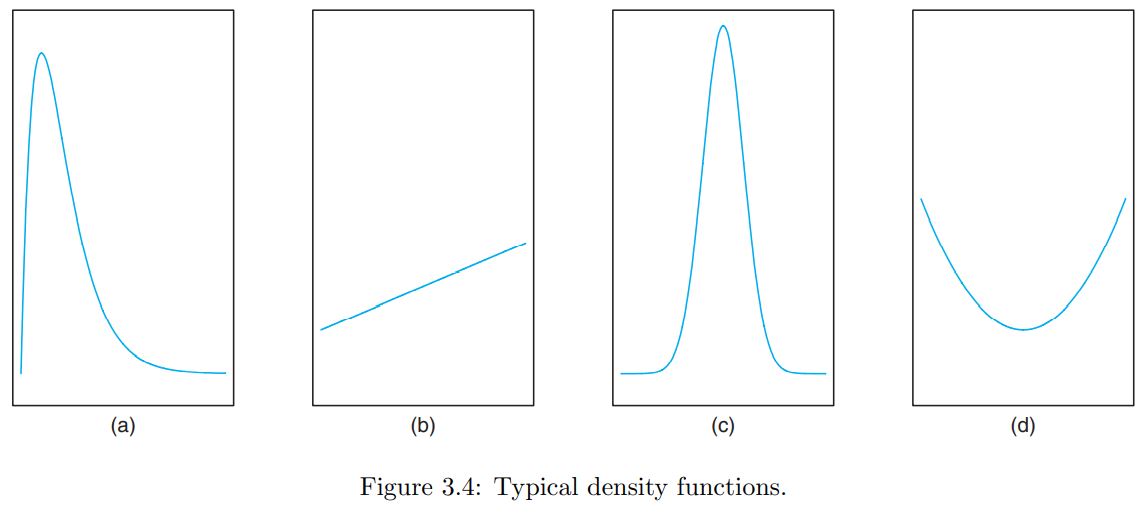
In Continuous RV, we assign a probability of 0 to the event. And its probability distribution cannot be given in tabular form. (확률 분포를 표로 적을 수 없다.) However, it can be stated as a formula $f(x)$. We call that formula as a <probability density function>!
Definition. Probability Density Function
The function $f(x)$ is a <Probability Density Function> (PDF) for the continuous RV $X$, defined over the set of real numbers, if
- \[f(x) > 0, \quad \mbox{for all } x \in R\]
- \[\int^{\infty}_{-\infty} f(x) \; dx = 1\]
- \[P(a < X < b) = \int^b_a f(x) \; dx\]
Definition. Cumulative Distribution Function for Continuous RV
The <cumulative distribution function> $F(x)$ of a continuuous RV $X$ with density function $f(x)$ is
\[F(x) = P(X \le x) = \int^x_{-\infty} f(t) \; dt, \quad - \infty < x < \infty\]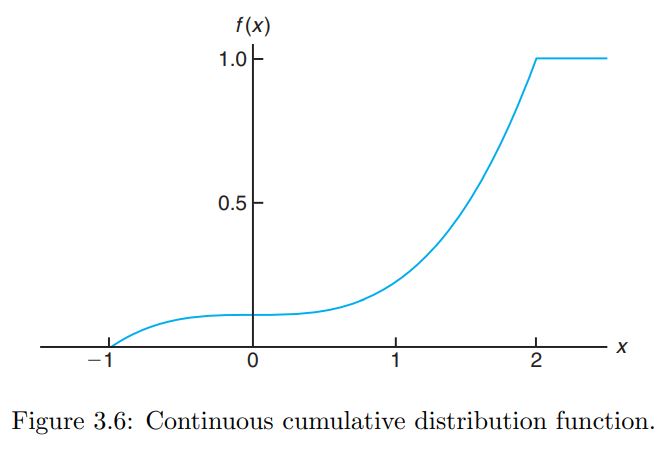
Continuous RV에서의 CDF는 적분으로 정의되기 때문에 CDF $F(x)$를 통해 PDF $f(x)$를 얻을 수 있다!!!
\[f(x) = \frac{dF(x)}{dx}\](단, $F(x)$의 derivative가 존재해야 한다.)
지금까지는 하나의 <Random Variable>이 $X$ 하나인 상황을 다뤘다면, 이어지는 내용에선 <Random Variable>이 $X$, $Y$ 두 개인 상황을 다룬다! 이것을 <Joint Probability Distribution>이라고 한다!
