Disjoint Set & Path Compression
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Kruskal’s Algorithm & Prim’s Algorithm에서 이어지는 포스트입니다.
Disjoint Set
이번 포스트에서는 <Disjoint Set>이라는 자료구조에 대해 살펴본다. 수학의 Set을 자료구조로 구현한 것이라고 생각하면 된다.
먼저 <disjoint set>의 구체적이 구현 없이 기본 연산들을 살펴보자.
- $\text{makeset}(x)$: create a new set containing $x$.
- $\text{find}(x)$: return the root node of the set containing $x$.
- $\text{union}(x, y)$: form a union of two sets containing $x$ and $y$.
흔히 집합의 기본 연산이라고 하면 집합 사이의 Intersection, Union, Difference를 생각하기 마련인데, 제시된 기본 연산들은 모두 노드 $x$를 인자로 받는 것을 볼 수 있다.
그리고 노드 $x$에 대해서는
- $\pi(x)$: pointer to its parent
- $\text{rank}(x)$: height of the subtree hanging from $x$ ($x$를 루트로 갖는 subtree의 높이)
사실 $\pi(x)$와 $\text{rank}(x)$는 <disjoint set>이 Tree 형태로 구현되어 있다는 것을 알아야 제대로 이해할 수 있다.
<disjoint set>의 기본 연산으로 어떻게 Tree 형태의 <disjoin set>이 만들어지는지 살펴보자. 👀
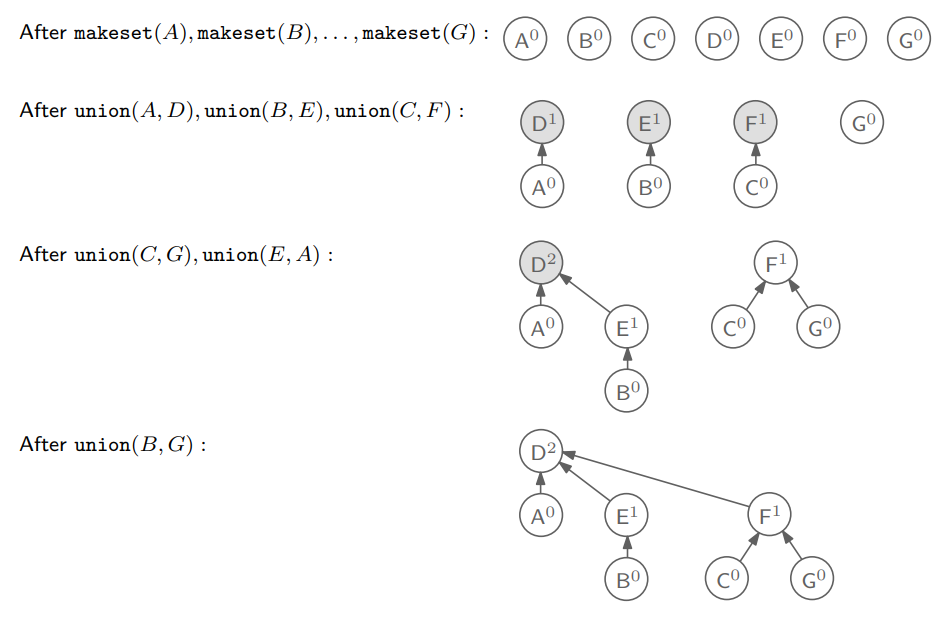
먼저 $\text{makeset}(x)$는 루트 노드만 있는 트리를 생성한다. 그리고 $\text{union}(x, y)$ 연산은 각 노드가 포함된 두 개의 트리를 하나의 트리로 병합한다. 이때 하나의 트리를 다른 트리의 subtree로 병합된다. 구체적으로 어떻게 $\text{union}(x, y)$로 트리를 병합하는지는 코드를 보며 이해해보자.
Algorithm $\text{makeset}(x)$
$\pi(x) \leftarrow x$
$\text{rank}(x) \leftarrow 0$
먼저 $\text{makeset}(x)$은 루트 노드만 있는 트리를 만든다. 루트 노드는 부모가 자기 자신을 가리키기 때문에 $\pi(x)$는 자기자신인 $x$이다.
Algorithm $\text{find}(x)$
while $x \ne \pi(x)$
do $x \leftarrow \pi(x)$
return x
노드 $x$의 루트 노드를 반환하는 $\text{find}(x)$는 $\pi(x)$를 순회하며 쉽게 구할 수 있다.
Algorithm $\text{union}(x, y)$
$r_x \leftarrow \text{find}(x)$
$r_y \leftarrow \text{find}(y)$
if $r_x = r_y$ // already in same set
them return
if $\text{rank}(r_x) > \text{rank}(r_y)$
then $\pi(r_y) \leftarrow r_x$ // attach $r_y$ to $r_x$
else if $\text{rank}(r_x) < \text{rank}(r_y)$
$\pi(r_y) \leftarrow r_x$ // attach $r_x$ to $r_y$
else
$\pi(r_y) \leftarrow r_x$
$\text{rank}(r_y) \leftarrow \text{rank}(r_y) + 1$
즉, 두 노드 $x$, $y$의 루트 노드를 $\text{find}()$로 찾은 후, 두 set의 크기를 $\text{rank}(r_x)$, $\text{rank}(r_y)$로 얻어 $\text{rank}$가 큰 집합에 작은 집합을 붙이는 방식으로 $\text{union}()$을 수행한다.
<disjoint set>의 주요한 연산인 $\text{union}$과 $\text{find}$에서 발견되는 성질을 나열하면 아래와 같다.
- For any $x$, $\text{rank}(x) \le \text{rank}(\pi(x))$
- If $x$ is not a root, $\text{rank}(x)$ will nenver change again.
- Rank changes only for roots. A non-root node never becomes a root.
- Any root node of rank $k$ has at least $2^k$ nodes in its tree.
- If there are $n$ elements overall, there can be at most $n/2^k$ nodes of rank $k$.
- The maximum rank is $\log n$, so the tree height $\le \log n$.
이 중에서 3번째 문장을 증명해보자.
[Proof by Induction]
- (Base) It holds for $k=0$
- Assume that the claim holds for $k-1$.
- A node $x$ of rank $k$ is created only by mergining two roots of rank $k-1$, each subtree consisting of $\ge 2^{k-1}$ nodes. Thus, $x$ has $\ge 2^k$ nodes in its subtree.
$\blacksquare$
마지막 4번째 문장은 두 노드가 동일 집합에 속하는지를 판단하는데 $O(\log n)$의 비용이 필요함을 의미한다. 그래서 Kruskal Algorithm에서는 MST를 만들기 위해 union-find로 동일 집합에 속하는지 계속 체크하게 되는데, 이 작업에 $O(E \log V)$ 만큼의 비용이 발생한다.
Path Compression
놀랍게도 <disjoint set>은 Path Compression이라는 작업을 병행해주면 훨씬 적은 비용으로 union-find 작업을 수행할 수 있다! 😲 Path Compression은 <disjoint set>의 트리의 높이를 짧게 유지해주는 방법이다.
Path Compression은 $\text{find}(x)$ 연산을 수행하기만 하면 된다!
Algorithm $\text{find}(x)$
if $x \ne \pi(x)$
then $\pi(x) \leftarrow \text{find}(\pi(x))$
return $\pi(x)$
$\text{find}(x)$ 함수가 재귀함수의 꼴이 되어서 헷갈릴 수도 있지만, 핵심은 노드 $x$가 루트 노드도록 만든다는 것이다. $\text{find}(x)$가 항상 루트 노드를 반환한다는 사실을 잘 해석하면 된다.
그림으로 보면 아래와 같다.
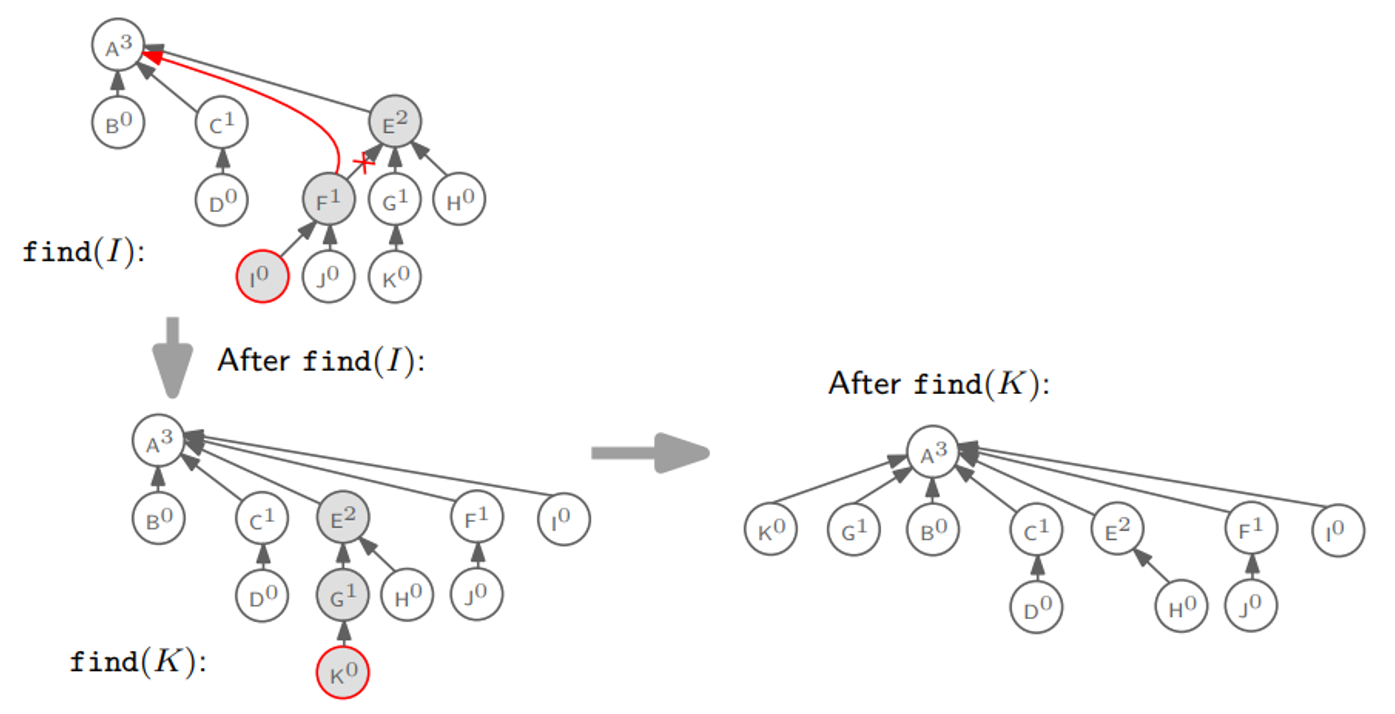
Time Complexity
Path Compression을 도입하면서 더이상 $\text{find}$의 비용은 $O(\log n)$보다 작아지게 되었다. 그렇담 시간 복잡도를 어떻게 구해야 할까?
잠깐! 🖐 시간 복잡도를 유도하기 전에 <interval>이라는 개념에 대해 살펴보고 가자. interval $I_k$는 아래와 같이 정의한다.
\[I_k = \left\{ k+1, k+2, ..., 2^k \right\}\]그래서 값을 나열해보면,
\[\begin{aligned} I_0 &= \left\{ 1 \right\} \\ I_1 &= \left\{ 2 \right\} \\ I_2 &= \left\{ 3, 4 \right\} \\ I_4 &= \left\{ 5, 6, ..., 15, 16 \right\} \\ I_{16} &= \left\{ 17, 18, ..., 2^{16} \right\} \\ &... \\ I_i &= \left\{i+1, ..., 2^i\right\}\\ I_{2^i} &= \left\{ ... \right\} \end{aligned}\]자! 다시 disjoint set의 tree로 돌아와보자. $n$개 노드를 갖는 disjoint set의 tree의 $\text{rank}$는 아래의 범위를 갖는다.
\[0 \le \text{rank}(x) \le \log n\]우리는 $\text{rank}(x)$를 앞에서 구한 <interval>로 분배할 것이다. 이때 $\text{rank}(x)$가 어느 <interval>에 속하는지는 아래의 함수로 쉽게 알 수 있다.
\[\log^{*} n\]이 $\log^{*}$ 함수는 “number of successive $\log$ operation”을 계산하는 함수로 정수 $n$에 $\log$을 몇번 취해야 $\le 1$이 되는지를 계산하는 함수다. 점화식으로 표현하면 아래와 같다.
\[\log^{*} n = \begin{cases} 0 & \text{for} \; n \le 1 \\ 1 + \log^{*}(\log_2 n) & \text{for} \; n > 1 \end{cases}\]$16 = 2^{2^{2}}$를 예로 들자면,
\[\log^{*} 2^{2^{2}} = 1 + \log^{*} 2^{2} = 2 + \log^{*} 2 = 3\]이 된다. 이것은 곧 $16$이 3번째 <interval>인 $I_4$에 속한다는 것을 말한다.
<interval>이니 $\log^{*}$ 함수니 와닿지 않을 수 있다. 이 문단에서 얻을 것은 $\log^{*}$ 함수로 $\text{rank}(x)$가 몇 번째 <interval>에 속하는지 알 수 있다는 것과 이를 활용하면 두 노드 $x$, $y$의 $\text{rank}$ 값이 서로 같은 <interval>에 속하는지 아닌지를 $\log^{*}$ 함수로 쉽게 알 수 있다는 것만 잘 이해하면 된다 👏
우리는 $\text{find}$ 연산과 $\text{union}$ 연산이 섞여있는 일련의 연산을 살펴본다고 하자. 일단 처음에는 empty tree에서부터 시작한다. 일련의 연산에는 $\text{find}$ 연산과 $\text{union}$ 연산이 섞여있지만 우리는 $\text{find}$ 연산을 $m$번 실행한다고 생각할 것이다. 왜냐면 $\text{union}$ 연산도 결국은 $\text{find}$를 쓰기 때문이다.
어떤 노드 $u$에서 $\text{find}$를 통해 루트 노드까지 도달하는 과정을 생각해보자. 부모 노드를 거슬러 올라갈 때마다 우리는 다음의 두 가지 경우를 마주한다.
- $x$ and $\pi(x)$ belong to the different interval.
- $x$ and $\pi(x)$ belong to the same interval.
우리는 각 경우에 대해 걸리는 비용을 $T_1$, $T_2$로 적고, $\text{find}$로 루트 노드에 도달하는 과정의 총 비용 $T$를 유도할 것이다.
\[T = T_1 + T_2 = \sum (1) + \sum (2)\]1. $x$ and $\pi(x)$ belong to the different interval
$n$의 노드를 가진 Tree가 있다고 생각해보자. 최대 $\text{rank}$가 $\log n$이기 때문에 interval의 갯수는 $\log^{*} n$이다. 그래서 한번의 $\text{find}$에서 interval이 바뀌는 횟수도 최대 $\log^{*} n$번 만큼 일어난다. 처음에 $\text{find}$ 연산을 $m$번 실행한다고 했으므로 비용 $T_1$은
\[T_1 = O(m \cdot \log^{*} n)\]이다.
2. $x$ and $\pi(x)$ belong to the same interval
같은 interval에 속하는 $\text{rank}$는 모두 같은 $\log^{*}$ 값을 가진다. 그럼 $n$개 노드를 가진 tree에서 같은 interval에 속하게 되는 노드의 갯수는 총 몇 개나 될까?
<disjoint set>의 자료형의 성질 중 마지막 4번재 성질에서 $\text{rank}$가 $k$인 노드가 최대 $n/2^{k}$개 만큼 존재한다는 것을 안다. 그래서 한 interval 안에 속하는 노드의 총 갯수는
\[\frac{n}{2^{k+1}} + \frac{n}{2^{k+2}} + \cdots\]만큼 존재할 것이다. 그리고 이것은
\[\begin{aligned} &\frac{n}{2^{k+1}} + \frac{n}{2^{k+2}} + \cdots \\ &= n \cdot \left( \frac{1}{2^{k+1}} + \frac{1}{2^{k+2}} + \cdots \right) \\ &= \frac{n}{2^{k+1}} \cdot \left( 1 + \frac{1}{2} + \frac{1}{2^2} + \cdots\right) \\ &= \frac{n}{2^{k+1}} \cdot 2 = \frac{n}{2^k} \end{aligned}\]가 된다. 즉, interval $I_k$에 대해 $\left| I_k \right| = n/2^k$라는 말이다.
그럼 어떤 노드 $u$에서 $\text{find}$를 시작해서 다른 interval에 속하게 될 때까지 총 몇 번의 $\text{find}$ 함수 호출이 필요할까? $\text{find}$ 호출 1회당 하나씩 $\text{rank}$가 하나씩 줄어간다고 생각하면 $\le 2^{k}$번의 $\text{find}$ 호출로 다른 interval에 속하는 노드를 만나게 된다.
그래서 interval $I_k$에 속하는 모든 노드들에 대해 이것들을 다른 interval에 속하게 하려면 총 $(\le 2^{k}) \times n/2^k = (\le n)$번 만큼의 $\text{find}$ 호출이 필요하다.
이것은 하나의 interval에 대해 필요 한 $\text{find}$ 호출의 총 횟수이다. Tree에 $\log^{*} n$ 만큼의 interval이 있으므로 $(\le n) \times \log^{*} n$ 만큼의 $\text{find}$ 호출이 필요하다.
\[T_2 = O(n \cdot \log^{*} n)\]이제 $T_1$, $T_2$의 비용을 더해서 일련의 $\text{find}$, $\text{union}$ 연산에 드는 비용을 구해보자. 전체 연산에 필요한 총 비용은
\[O(m \cdot \log^{*} n) + O(n \cdot \log^{*} n) = O(m \cdot \log^{*} n)\]이다. 여기서 우리는 연산의 총 비용에 연산의 횟수 $m$을 나누어 amortized cost를 유도할 것이다. 따라서 $\text{find}$ 연산의 amortize cost는
\[O(m \cdot \log^{*} n) / m = O(\log^{*} n)\]이다!
최종적으로 구해진 $\text{find}(x)$의 비용인 $O(\log^{*} n)$는 정말 작은 비용이다. $n = 2^{16}$일 때도 4밖에 안 되기 때문에 사실상 상수 비용이라고 보면 된다.
이것으로 <disjoint set> 자료구조에 대해 살펴보았다. disjoint set을 통해 그래프에서 사이클이 존재하는지 확인할 수 있기 때문에 MST 외에도 충분히 활용할 수 있다.
다른 포스트에서 <Heap> 자료구조의 구현에 대해 기술한 Implementations of Heap 포스트도 있으니 알고리즘 문제해결에 쓰는 자료구조가 더 궁금하다면 추천한다.
