Splines Method (2)
2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
이 포스트는 Regression Spline과 이어지는 내용입니다 😊
Non-parameteric Logistic Regression
본래 <Binary Logistic Regreeion>은 아래와 같이 모델링한다.
\[\log \frac{P(Y = 1 \mid X=x)}{P(Y = 0 \mid X=x)} = \beta^T x\]위의 식을 다시 잘 정리하면 아래와 같다.
\[P(Y = 1 \mid X = x) = \frac{e^{\beta^T x}}{1 + e^{\beta^T x}}\]<Non-parametric (binary) logistic regression>은 위의 식에서 $\beta^T x$를 $f(x)$로 대체한다!!
\[P(Y = 1 \mid X = x) = \frac{e^{f(x)}}{1 + e^{f(x)}}\]이때, $f(x)$는 현재 모르는 상태로 우리가 estimation 해야 하는 대상이다!!
정규 수업에서는 $f(\cdot)$를 추정하는 방식으로 아래의 “penalized log-likelihood function”을 Maximize 하는 것을 제시한다.
\[\ell_\lambda (f) = \sum^n_{i=1} \left[ y_i f(x_i) - \log (1 + e^{f(x_i)}) \right] - \frac{\lambda}{2} \int \left\{ f''(t) \right\}^2 \; dt\]복잡하게 생각하기 보다는 <smoothing spline>과 비슷한 형태라고 인식 해두자!
Multi-dimensional Splines
지금까지 살펴본 <Spline Method>는 모두 1-dimensional spline model이었다. 하지만, 많은 경우 feature의 상호작용을 고려하는 multi-dimensional한 접근을 필요로 한다.
<Multi-dimensional Spline>은 아래와 같이 모델링 한다.
\[f(X) = \sum^{M_1}_{i=1} \sum^{M_2}_{j=1} \; \theta_{ij} \cdot g_{ij} (X)\]where $g_{ij}(X)$ is the tensor product of basis function, defined by
\[g_{ij}(X) = h_{1i} (X_1) \cdot h_{2j} (X_2)\]즉, “multi-dimensional spline”은 두 basis spline을 곱한 것을 basis function으로 삼는다는 말이다!
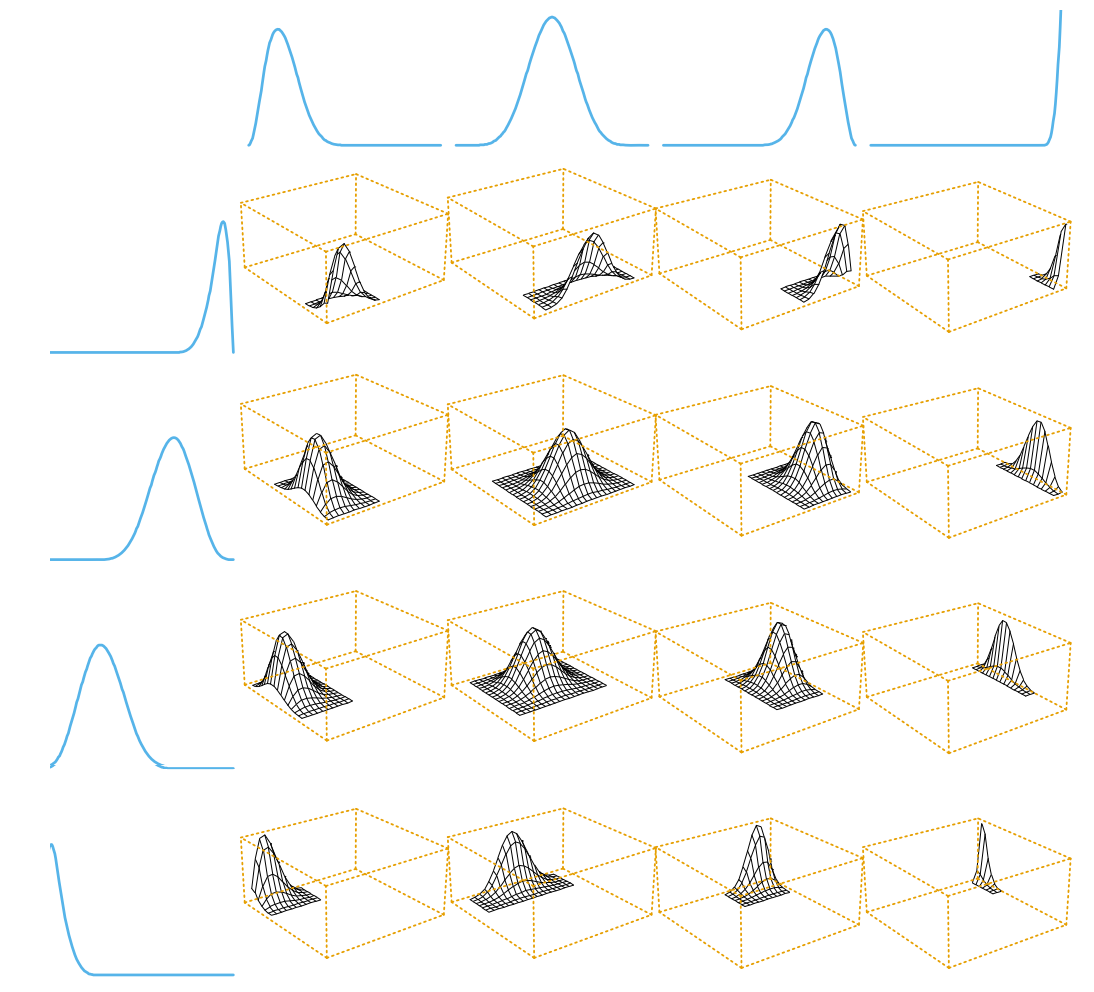
위와 같은 방식으로 접근하면, 2-dim 뿐만 아니라 d-dim까지도 쉽게 generalization 할 수 있다.
그러나 input variable의 수 $d$가 증가한다면, multi-dimensional model이 필요로 하는 basis function은 exponential하게 증가한다. 이것은 계산량 뿐만 아니라 curse of dimensionality 등의 문제를 동반한다.
이런 문제를 해결하기 위한 대안으로 1991년, <MARS; Multi-variate Adaptive Regression Spline>가 제시되었다.
또, 정규 과정의 마지막 즈음에 다룰 <Additive Model> 역시 이런 multi-dimensional model의 문제를 해결하는 대안이 된다.
이어지는 포스트에서는 KNN 기반의 non-parametric method에 대해 살펴보겠다.
