KNN & kernel method
2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
이 포스트는 Regression Spline과 Spline Method (2)이어지는 내용입니다 😊
KNN; K-Nearest Neighbor method
Regression function $f(x) = E(Y \mid X=x)$를 모델링 하는 가장 자연스러운 접근중 하나는 바로 $x$에 가장 가까운 $k$개의 점으로 평균을 내는 <KNN>이다.
\[\hat{f}(x) = \text{Avg} \, (y_i \, \mid \, x_i \in N_k(x))\]where $N_k(x)$ is the set of $k$ points nearest to $x$.
이렇게 KNN을 쓸때 깔린 가정은 “추정하려는 함수 $f(x)$가 smooth 하다”이다.
KNN의 parameter인 $k$는 model complexity를 컨트롤 한다.
- small $k$: model complexity ▲, bias ▼, variance ▲ // make ziggle model
- Large $k$: model complexity ▼, bias ▲, variance ▼ // make smooth model
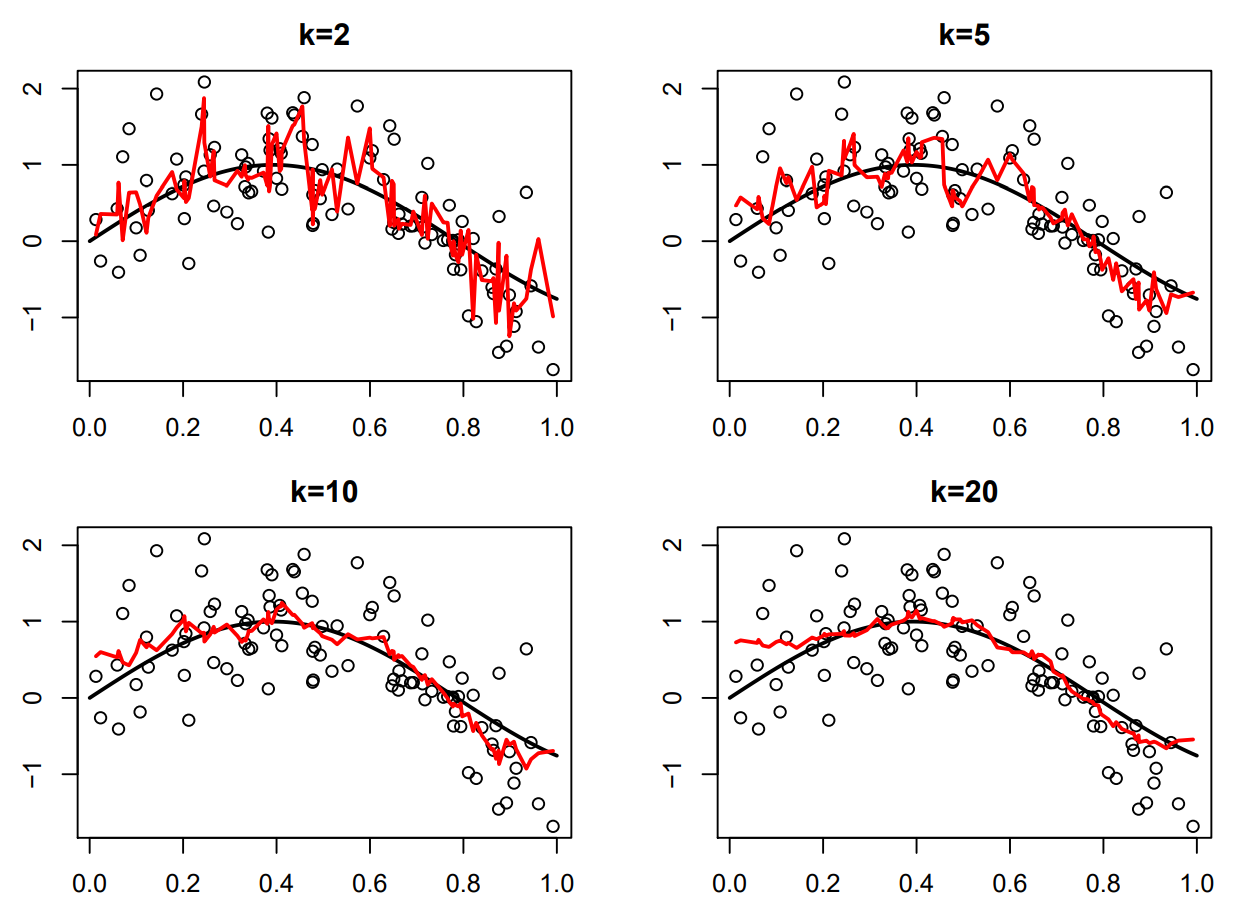
[Problem 😱] KNN $\hat{f}(x)$ is not smooth and not continuous!!
KNN의 문제를 해결하기 위해 도입하는 것이 바로 <kernel method>다!
Kernel Method
KNN의 식을 다시 기술해보면 아래와 같다.
\[\hat{f}(x) = \frac{\displaystyle \sum^n_{i=1} \, K_k (x, x_i) \cdot y_i}{\displaystyle \sum^n_{i=1} \, K_k (x, x_i) }\]where $K_k (x, x_i) = I(x_i \in N_k (x))$.
<kernel method>의 메인 아이디어는 KNN에서 $I(x_i \in N_k(x))$를 다른 smooth function $K_{\lambda}(x, x’)$로 대체한다는 것이다!! 이때의 그 smooth function $K_{\lambda}(x, x’)$를 <kernel function>이라고 한다!!
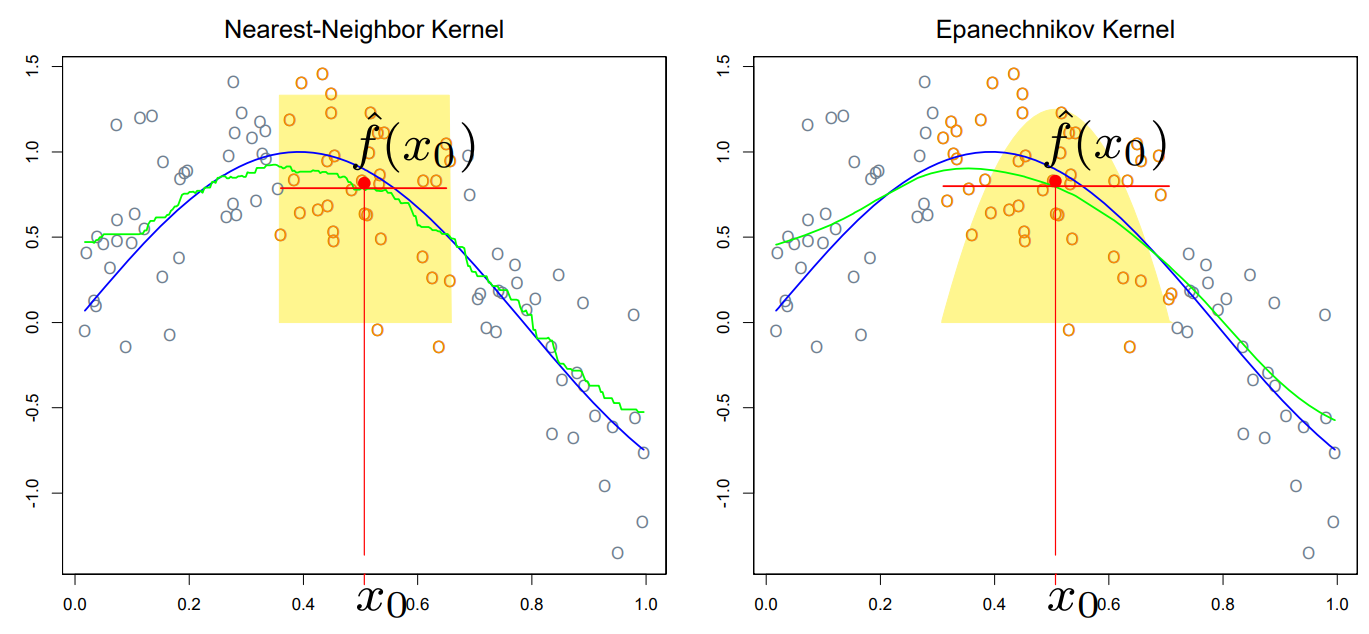
위의 그림은 <kernel function> 중 하나인 <Epanechnikov kernel>을 시각화한 것이다.
즉, <kernel method>는 equally weighting 하는 KNN과 달리, kernel에 따라 가까이 있는 point에는 더 큰 weight을 부여해주는 역할을 한다.
Q. <kernel method>를 적용한 그림에서 boundary 쪽을 보면, estimated curve가 약간 올라가 있는 것을 볼 수 있다. 이것은 왜 발생하는 것이며, 이 문제는 dataset에 상관없이 일어나는 <kernel method>의 본질적인 문제인가?
A. 아무리 <kernel method>라고 해도 boundary problem에서 자유로울 순 없다. 이것은 <kernel method>의 본질적인 문제다.
// 추가로 함수의 가운데 부분에서도 추정이 정확하지 않은 것을 볼 수 있다 😥
Nadaraya-Watson Estimator
For a given kernel $K_\lambda$, <Nadaraya-Watson Estimator> is
\[\hat{f}(x) = \frac{\displaystyle \sum^n_{i=1} K_{\lambda} (x, x_i) \cdot y_i}{\displaystyle\sum^n_{i=1} K_{\lambda} (x, x_i)}\]이 <NW Estimator>에 사용되는 커널 중 유명한 것은 대부분 아래의 형태를 지닌다.
\[K_{\lambda} (x, x') = D \left( \frac{\left| x - x' \right|}{\lambda} \right)\]where $D$ is a non-negative decreasing on $[0, \infty)$.
$D$는 대충 종모양의 우함수라고 생각하면 된다. <Epanechnikov kernel>가 대표적인 예시다.
Examples.
- Epanechnikov kernel
- Tri-cube kernel
- Gaussian kernel
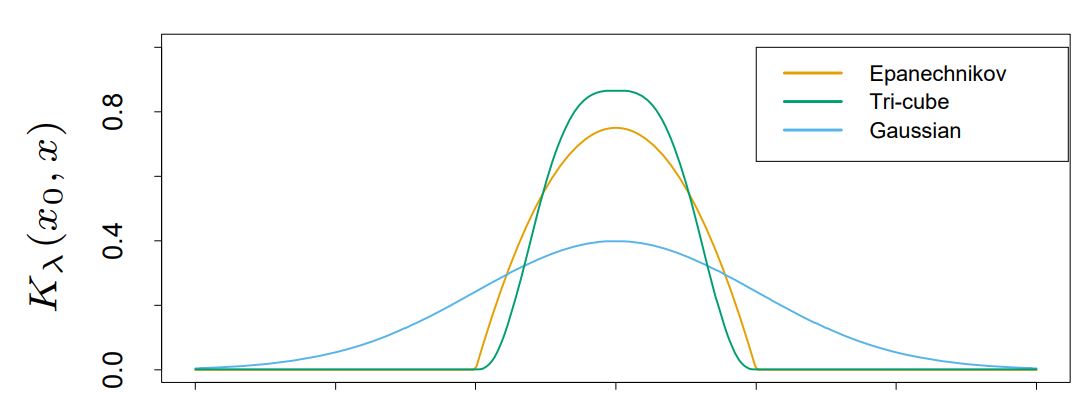
$\lambda$는 일종의 tuning parameter로, scale을 조정하는 기능을 한다; bandwidth (smoothing) parameter.
- small $\lambda$: model complexity ▲, bias ▼, variance ▲ // make ziggle model
- Large $\lambda$: model complexity ▼, bias ▲, variance ▼ // make smooth model
// KNN의 $k$처럼 model complexity를 결정하는 역할을 한다!!
💥 Problem: <Nadaraya-Watson Estimator> has large bias around the boundary 😥
Local Linear Regression with kernel method
kernel method를 쓰는 <Nadaraya-Watson Estimator>에선 “curvurse를 제대로 catch하지 못 한다”, “boundary에서 bias가 크다” 등의 문제가 있었다. 이 문제를 해결하기 위한 방법을 살펴보자!
지금까지의 <kernel method>는 사실 weighted local constant fitting을 한 것이다. 즉, “local constant fitting”을 하긴 했는데, kernel function으로 weighting을 했다는 말이다. 그래서 이번에는 constant fitting 대신에 linear fitting 하는 방법을 도입하게 된다!
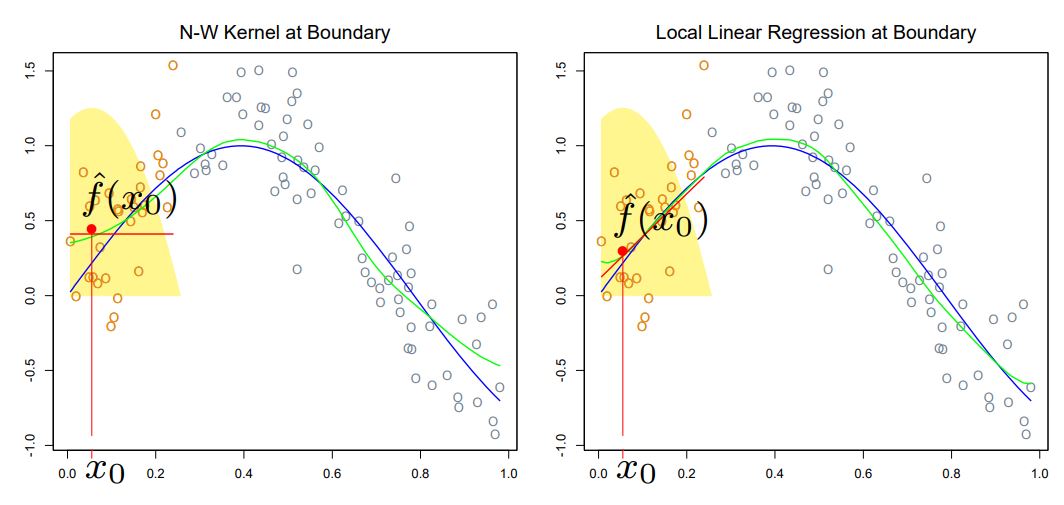
👀 <local linear regression>이 <NW estimator> 보다 boundary에서 훨씬 bias가 줄어든 것을 확인할 수 있다!! 👀
Find a local linear estimator $\hat{f}(x) = \alpha(x) + \beta(x)\cdot x$ where
\[\underset{\alpha(x), \, \beta(x)}{\text{argmin}} \; \sum^n_{i=1} \; K_{\lambda} (x, x_i) \, \left[ y_i - \alpha(x) - \beta(x) \cdot x_i \right]^2\]위의 식은 local 구간 중 하나의 구간에 대한 estimated function $\hat{f}(x)$을 기술한 것이다. 이것을 전체 구간으로 확장해서 행렬의 형태로 기술하면 아래와 같다.
Let $\mathbf{W}(x) = \text{diag} (K_\lambda (x, x_i))$, and $\mathbf{B}$ be $n\times 2$ with $i$-th row $b(x_i)^T$, where $b(x) = (1, x)^T$.
Then,
\[\hat{f}(x) = b(x)^T \cdot \left( \mathbf{B}^T \mathbf{W}(x) \mathbf{B} \right)^{-1} \cdot \mathbf{B}^T \mathbf{W}(x) \mathbf{y}\]식이 많이 복잡하다. 조금 간단하게 보려면, weight 부분인 $\mathbf{W}(x)$를 빼고 식을 먼저 이해하는게 좋을 것 같다.
이 <local linear regression>의 아이디어를 확장에 <local polynomial regression>으로 확장해볼 수도 있다!!
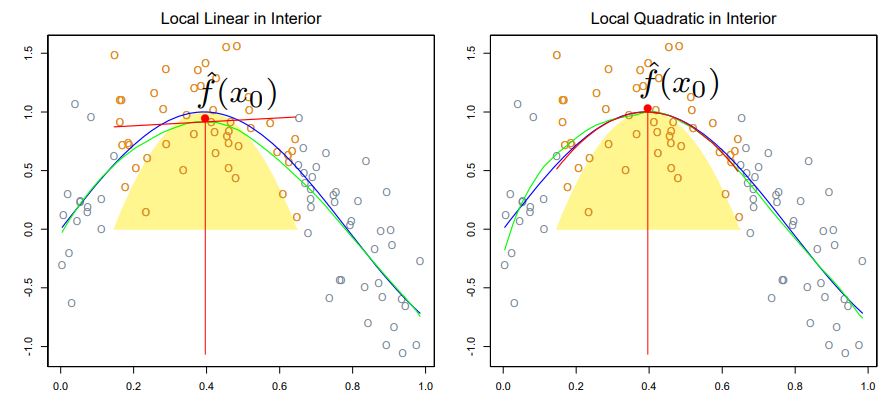
👀 <local quadratic regression>이 <local linear regression>보다 curverture가 있는 부분을 더 잘 fitting 하는 것을 볼 수 있다. 👀
Q. 지금까지의 살펴본 것을 종합해보면, <local constant fit> 보단 <local linear fit>이 좋았다. 또, <local quadratic fit>이 더 좋았다. 그렇다면, polynomial fitting의 차수가 높을 수록 좋은 것 일까?
A. NO!!!
상황에 따라 다르다!!! 아래의 그림을 살펴보자.
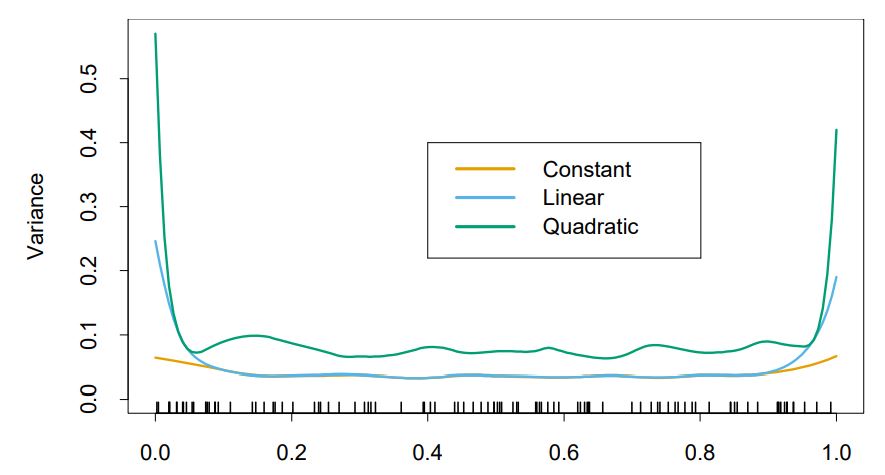
이 경우, <constant fit>이 가장 좋은 결과를 보였다. 또, boundary에서 <quadratic fit>은 큰 variance을 보이는 걸 확인할 수 있다. // 위 그림에선 bias는 똑같은데 variance는 quadratic이 가장 컸다.
이것은 결국 <bias-variance tradeoff>로 higher polynomial은 bias를 잘 맞출 수 있어도 variance가 높아지는 경향이 있다.
따라서, higher polynomial로 fitting 하는 전략이 항상 우세하다고 말할 수는 없는 것이다.
💥 당연하게도 dataset의 true relation의 curvurture가 작을 수록 linear fit이 일반적으로 더 좋은 성능을 낸다.
Local Likelihood Approach for logistic regression
이번에는 <spline method>에서 살펴봤던 <non-parametric (binary) logistic regression> 모델에 <kernel method>를 적용해보자.
<logistic regreeion>에서는 $f(x) = x^T \beta(x)$를 구했었다. 여기에 <kernel method>를 추가하면, 아래의 최적화 문제를 풀어 $\hat{\beta}(x)$를 구하는 문제가 된다.
\[\hat{\beta}(x) = \underset{\beta}{\text{argmax}} \; \sum^n_{i=1} \; K_{\lambda}(x, x_i) \cdot \ell (y_i, x_i^T\beta)\]where $\ell(y, f(x)) = y \cdot f(x) - \log (1 + e^{f(x)})$.
Kernel method with $p > 1$
지금까지 살펴본 <kernel method>는 input variable의 차원 $p$가 1인 경우 였다. 이번에는 $p$가 1 이상인 경우, <kernel method>에 대한 식을 살펴보겠다.
일반적으로 $p$가 커지면, “neighborhood”의 개념이 잘 동작하지 않게 된다. (curse of dimensionality) 그래서 $p > 1$에서는 “neighbor”를 단순히 구하는 것보단 어떤 structure를 가정하고 접근한다.
\[K_\lambda (x, x') = D \left( \frac{(x-x')^T A (x - x')}{\lambda} \right)\]이런 “structured assumption”의 예시로는
- $f(X) = \alpha + \beta^T X$; linear structure
- $f$ is a super-smooth function
- $f$ can be represented by few basis functions
- Additive model: $f(X_1, \dots, X_p) = \alpha + f_1(X_1) + \cdots + f_p(X_p)$
- …
이 중에서 마지막 접근인 <Additive Model>이 바로 다음 포스트에서 다룰 내용이며, $p$ 차원 함수를 추정하는 어려운 문제를 1차원 함수 $p$개를 추정하는 문제로 가정해 해결하는 접근법이다.
👉 Additive Model 🔥
