Variance Estimation
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Interval Estimation 포스트에서 다룬 <Interval Estimation>을 특정 상황에 어떻게 적용할 수 있는지를 다루는 포스트입니다.
Single Sample Estimation: Variance Estimation
Let $X_1, \dots, X_n$ be a random sample from $N(\mu, \sigma^2)$.
Q. Find $100(1-\alpha)\%$ confidence interval for $\sigma^2$.
1. choose a point estimator for $\sigma^2$.
\[S^2 = \frac{1}{n-1} \cdot \sum^n_{i=1} (X_i - \bar{X})^2\]and also
\[\frac{(n-1) S^2}{\sigma^2} \; \sim \; \chi^2 (n-1)\]2. Find confidence interval by using $\dfrac{(n-1) S^2}{\sigma^2} \; \sim \; \chi^2 (n-1)$.
\[1 - \alpha = P \left( \chi^2_{1-\alpha/2} (n-1) \; \le \; \frac{(n-1)s^2}{\sigma^2}\; \le \; \chi^2_{\alpha/2} (n-1)\right)\]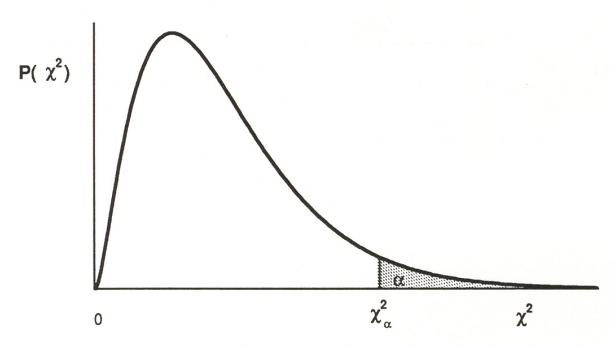
Therefore, the confidence interval for $\sigma^2$ is
\[\left( \frac{(n-1)\cdot s^2}{\chi^2_{\alpha/2}}, \frac{(n-1)\cdot s^2}{\chi^2_{1 - \alpha/2}} \right)\]where $\chi^2_{\alpha/2}$ and \(\chi^2_{1-\alpha/2}\) are $\chi^2$-values with $n-1$ dof.
💥 NOTE: $X_1, \dots, X_n$ should follow $N(\mu, \sigma^2)$.
💥 NOTE: $\chi^2$ distribution is NOT symmetric!
Two Samples Estimation: The ratio of two variances
Let $X_1, \dots, X_{n_1}$ be random samples from $N(\mu_1, \sigma_1^2)$.
Let $Y_1, \dots, Y_{n_2}$ be random samples from $N(\mu_2, \sigma_2^2)$.
Supp. $X_i$s and $Y_j$s are independent.
Q. Find $100(1-\alpha)\%$ confidence interval for $\sigma_1^2 / \sigma_2^2$.
A. We can use $s_1^2 / s_2^2$ instead!!
\[\frac{s_1^2 / \sigma_1^2}{s_2^2 / \sigma_2^2} \; \sim \; F(n_1-1, n_2-1)\]따라서,
\[1 - \alpha = P \left( f_{1-\alpha/2} \, (n_1 - 1, n_2 - 1) \; \le \; \frac{s_1^2 / \sigma_1^2}{s_2^2 / \sigma_2^2} \; \le \; f_{\alpha/2} \, (n_1 - 1, n_2 - 1) \right)\]Note that $f_{1-\alpha/2} \, (n_1 - 1, n_2 - 1) = \dfrac{1}{f_{\alpha/2} \, (n_2 - 1, n_1 - 1)}$.
Therefore, the confidence interval for $\sigma_1^2 / \sigma_2^2$ is
\[\left( \frac{s_1^2}{s_2^2} \cdot \frac{1}{f_{\alpha/2} \, (n_1 - 1, n_2 - 1)}, \; \frac{s_1^2}{s_2^2} \cdot f_{\alpha/2} \, (n_2 - 1, n_1 - 1) \right)\]지금까지 “추정(Statistical Estimation)” 과정에 대해 살펴보았다. $\bar{x}$와 $s^2$와 같이 Point Estimator를 구하는 경우도 있었고, $\bar{x} \pm z_{\alpha/2} \cdot s / \sqrt{n}$ 과 같이 Interval Estimator를 구하는 경우도 있었다. 또, Single Sample에서 Estimator를 구하는 것도 있었고, Two Samples에서 Estimator를 구하는 것도 있었다.
그러나 지금까지 살펴본 방식 외에도 또다른 Estimation 방법이 있다 😲 <MLE; Maximum Likelihood Estimation>는 Sample Distribution을 재현할 확률이 가장 높은 Parameter $\theta$를 찾는 방식으로 Estimator를 찾는다. <MLE>는 당연히 Point Estimator를 제시하며, 그 과정에서 $\theta$에 대해 편미분을 수행한다.
