Sample Mean Test
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Sample Mean Test
평균(Mean)에 대한 검정은 추정에서와 비슷하게, $\sigma^2$을 아는지 여부에 따라 다르게 접근한다.
$\sigma^2$ is known

1. 상황 인식
- $H_0: \mu=190$
- $H_1: \mu > 190$
$n=25$ and $\bar{x}=194$, and $\sigma^2 = 100$
2. Find a <Test Statistic>, and construct critical region
- Test Statistic: $\bar{x}$
- critical region: $\{ \bar{X} > C\}$
3. $\alpha$가 주어지지 않았으니, p-value를 구하자!
\[\begin{aligned} \alpha &= P(\bar{X} \ge 194 \mid \mu = 190) \\ &= P \left(\frac{\bar{X} - 190}{\sigma / \sqrt{n}} \ge \frac{194 - 190}{\sigma / \sqrt{n}} \right) \\ &= P(Z \ge 2) = 0.023 \end{aligned}\]4. 결정
- If $\alpha > 0.023$, reject $H_0$
- If $\alpha < 0.023$, fail to reject $H_0$
$H_1: \mu < \mu_0$인 것도, $H_1: \mu \ne \mu_0$ 경우도 비슷하게, 식을 잘 세워서 진행하면 된다!
정리하면 아래와 같다.
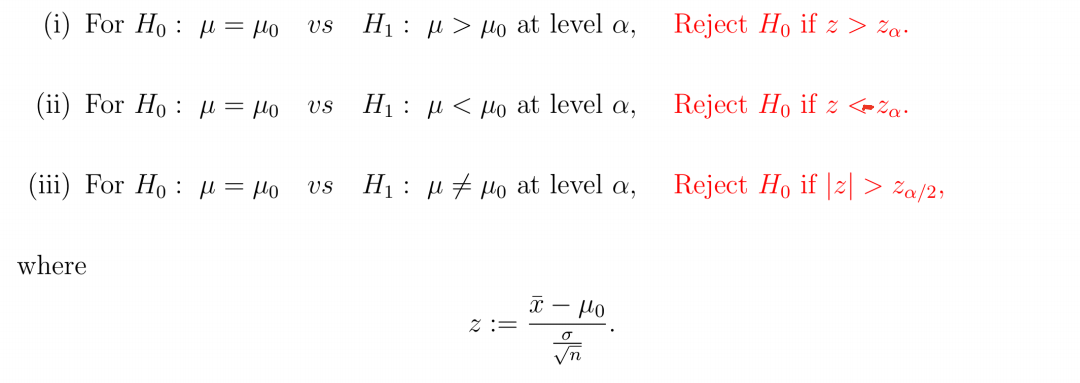
Quick Remark.
사실, “rejection region”과 “confidence interval”의 서로 Complement하다!!
만약, 우리가 얻은 sample mean $\bar{x}$이 $H_0$에서 가정한 $\mu$의 confidence interval에 포함된다면,
\[\bar{x} \in (\mu \pm z_{\alpha/2} \cdot \sigma/\sqrt{n}) \quad \text{or} \quad \bar{x} < \mu + z_{\alpha} \cdot \sigma/\sqrt{n} \quad \text{or} \quad \bar{x} > \mu - z_{\alpha} \cdot \sigma/\sqrt{n}\]우리는 $H_0$을 기각할 이유가 없다. 하지만, 만약 $\bar{x}$가 confidence interval을 벗어난다면, 우리는 우리가 설정한 $\mu$ 값을 의심하고, 또 기각해야 한다.
이것은 증명 방식 중 하나인 “귀류법”과 유사한데, “통게정 검정(Testing)”은 “확률”을 사용해 처음의 가정 $H_0$를 기각한다고 볼 수 있다!
$\sigma^2$ is unknown
만약, $\sigma^2$를 모른다면, 추정에서 했던 것처럼 <t-test>를 진행하면 된다. 너무 쉬우니 설명은 생-략 하겠다.
정리하면 아래와 같다.
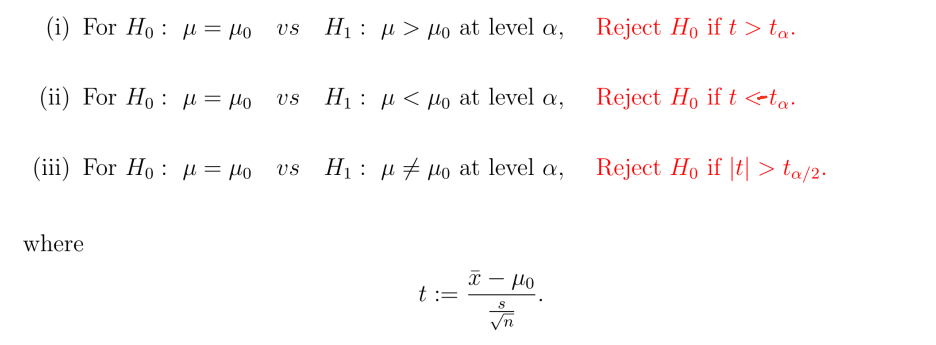
💥 주의!! 샘플은 반.드.시. Normal Distribution에서 추출되어야 한다!!
Two Samples Mean Test
이것도 사실 별거 없다. 그냥 추정해서 했던 것과 앞에서 했던 것을 잘 녹여서 검정을 수행하면 된다.
정리하면 아래와 같다.

마찬가지 방법으로 <Test for Paired Observations>에서도 그.대.로. 잘 수행하면 된다 😁
다음 포스트에서는 <검정력; power of test> $\beta$를 도입해 평균(Mean)에 대해 검정(Testing)을 수행할 때 필요한 Sample Size $n$을 결정하는 방법에 대해 살펴본다.
👉 Choice of Sample Size for Testing Mean
이번 포스트에서는 평균(Mean)에 대한 검정 방법에 대해 살펴봤다. 그렇게 어렵지 않았고, 추정(Estimation)에서 하던 걸, 절차에 맞게 수행해 해석해주면 되는 거였다. 이어지는 포스트에서는 비율(proportion)과 분산(variance)에 대한 검정을 살펴본다!
