Choice of Sample Size for Testing Mean
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Choice of Sample Size
실전에서는 실험(experiment)를 수행하기 전에 주어진 significance level $\alpha$ 아래에서 적절한 검정력을 갖는 sample size를 미리 설정한 후에 실험을 수행한다! 이 과정은 data-taking process 이전이라면, 반.드.시. 수행해야 하는 과정이다!
좋은 검정력을 얻기 위해 수행하는 “샘플의 수”를 결정하는 과정은 $\alpha$ 값과 $H_1: \mu = \mu_1$의 값을 고정하고 수행한다.
이때, <검정력>은 아래와 같다.
\[1 - \beta = P(\text{rejeect} \; H_0 \mid H_1 \; \text{is true})= P(\bar{X} > a \;\; \text{when} \;\; \mu = \mu_0 + \delta)\]이때, $\beta$는 T2 Error다!!

1. Set Hypothesis
- $H_0$: $\mu=190$ (cm)
- $H_1$: $\mu=195$ (cm)
2. we want
- $\alpha = 0.05$
- $1 - \beta \ge 0.9$
3. Evaluate T1 Error
\[\begin{aligned} \alpha &= P(\text{rejeect} \; H_0 \mid \mu = 190) \\ &= P \left( \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} > z_{\alpha} \right) \\ \end{aligned}\]위의 식은 어떤 $n$을 선택하더라도 항상 참인 명제다!
4. Evaluate T2 Error
$1 - \beta$ = (power at $\mu = \mu_1$) $\ge 0.9$.
\[1 - \beta = P \left( \text{reject}\; H_0 \mid \mu = \mu_1 \right) = P \left( \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} > z_{\alpha} \mid \mu = \mu_1 \right) \ge 0.9\]Now, let’s find $n$ which guarantees the eq. of (3) and (4).
\[\begin{aligned} P \left( \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}} < z_{\alpha} \mid \mu = \mu_1 \right) &\le \beta \\ P \left( \frac{\bar{X} - \mu_1 + \mu_1 - \mu_0}{\sigma/\sqrt{n}} < z_{\alpha} \mid \mu = \mu_1 \right) &\le \beta \\ P \left( z < z_{\alpha} - \frac{\mu_1 - \mu_0}{\sigma/\sqrt{n}} \right) &\le \beta \end{aligned}\]이때, $\mu_1 > \mu_0$ and $n$ is large,
\[z_{\alpha} - \frac{\mu_1 - \mu_0}{\sigma/\sqrt{n}} < 0\]More specifically,
\[z_{\alpha} - \frac{\mu_1 - \mu_0}{\sigma/\sqrt{n}} = - z_{\beta}\]Then, if we solve the above inequality, then we get a inequality for sample size $n$!
\[n \ge \left( \frac{(z_\alpha + z_\beta) \sigma }{\mu_1 - \mu_0} \right)^2\]교재에서는 위의 상황을 아래의 그림처럼 표현하고 있다!
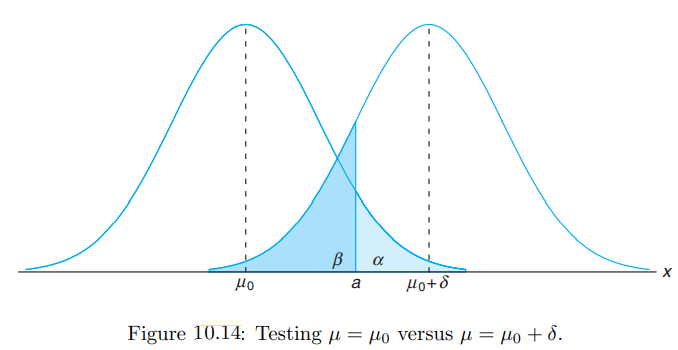
💥 (two-sided case) If $H_1$ is a form of $H_1: \mu \ne \mu_0$ at the level $\alpha$, and we want the power at $\mu = \mu_1$ to be at least $1 - \beta$?
이 경우에는 식이
\[n \ge \left( \frac{(z_{\alpha/2} + z_\beta) \sigma }{\mu_1 - \mu_0} \right)^2\]가 된다!
이어지는 포스트에서는 <Proportion>과 <Variance>의 검정에 대해 살펴본다!! 😆
