Chi-square Goodness-of-fit Test
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
<Proportion Test>의 내용을 먼저 살펴보고 오는 것을 추천한다. <Proportion Test>를 일반화한 것이 <Goodness-of-fit Test>이기 때문이다!
Introduction to Goodness-of-fit Test
<Goodness-of-fit Test; 적합도 검정>은 population distribution이 categorical variable을 가지는 경우, 예를 들어 Head-Tail의 동전 던지기, 주사위 던지기 등에서 사용하는 검정 기법이다. <Goodness-of-fit Test>는 카테고리 변수의 Sample Distribution (또는 Observed Distribution)이 가정한 Expected Distribution과 일치하는지를 결정한다.
먼저 아래의 예제를 풀면서, <Goodness-of-fit Test; 적합도 검정>에 대해 살펴보자.

1. 검정의 목표
- $H_0: p=0.8$
- $H_1: p \ne 0.8$
- significance level $\alpha$
2. 샘플링 상황
| - | made | missed | total |
|---|---|---|---|
| observed | 70 | 30 | 100 |
| expected under $H_0$ |
80 | 20 | 100 |
3. Test Statistic
이제 검정을 수행하기 위한 <Test Statistic>을 결정하자. sample proportion $\hat{p}$를 사용한다.
$\hat{p}$에 CLT를 적용하면, 아래와 같다.
\[\frac{\hat{p} - p}{\sqrt{p(1-p) / n}} \sim N(0, 1)\]이전의 <Proportion Test>에선 이걸 그대로 사용했다.
\[\text{reject} \; H_0, \quad \text{if} \quad \left| \frac{\hat{p} - p}{\sqrt{p(1-p) / n}} \right| > z_{\alpha/2}\]chi-square test에선 z-value에 제곱을 취한다.
\[\text{reject} \; H_0, \quad \text{if} \quad \left| \frac{\hat{p} - p}{\sqrt{p(1-p) / n}}\right|^2 > \left| z_{\alpha/2}\right|^2 = \chi^2_{\alpha}(1)\]<Goodness-of-fit Test>를 소개할 때도 말했듯이 <Goodness-of-fit Test>는 카테고리 변수에 대한 검정이다. 위의 식은 카테고리가 2개 뿐인 상황에서만 성립한다. 그래서 위의 식을 약간 변형해 <GOF Test>의 식을 유도해보자.
일단은 2개 카테고리에서 시작해보자.
\[\begin{aligned} \left| \frac{\hat{p} - p}{\sqrt{p(1-p) / n}}\right|^2 &= \frac{(\hat{p} - p)^2}{p(1-p)/n} \\ &= \frac{(x/n - p)^2}{p(1-p)/n} \\ &= \frac{(x/n - p)^2 \times n^2}{p(1-p)/n \times n^2} \\ &= \frac{(x - np)^2}{np(1-p)} \end{aligned}\]$\dfrac{1}{y(1-y)} = \dfrac{1}{y} + \dfrac{1}{1-y}$임을 이용해 식을 아래와 같이 분해한다.
\[\begin{aligned} \frac{(x - np)^2}{np(1-p)} &= \frac{(x-np)^2}{np} + \frac{(x-np)^2}{n(1-p)} \end{aligned}\]이때, $np$는 첫번째 카테고리에 대한 expected value인 $e_1 = 80$이고, $n(1-p)$는 두번째 카테고리에 대한 $e_2 = 20$이다. 마찬가지로, 분자의 $(x-np)^2$는 “observed value와 expected value의 차이 값”이다.
\[(x-np)^2 = (o_1 - e_1)^2\]그런데 $(x-np)^2$를 아래와 같이 표현하면, 두번째 observed value와 expected value의 차이 값으로 표현할 수도 있다!
\[(x-np)^2 = \left( (x-n) + (n-np) \right)^2 = (o_2 - e_2)^2\]식을 종합하면 아래와 같고,
\[\left| \frac{\hat{p} - p}{\sqrt{p(1-p) / n}}\right|^2 = \frac{(o_1 - e_1)^2}{e_1} + \frac{(o_2 - e_2)^2}{e_2}\]rejection criterion을 다시 쓰면,
\[\text{reject} \; H_0, \quad \text{if} \quad \sum_{i=1}^2 \frac{(o_i - e_i)^2}{e_i} > \chi^2_{\alpha}(1)\]2개 카테고리 예제를 $k$개 카테고리로 일반화 하여 기술해보자.
Definition. Test Statistic for Goodness-of-fit
<Goodness-of-fit>의 Test Statistic은
\[\chi^2 := \sum_{i=1}^k \frac{(o_i - e_i)^2}{e_i}\]where $o_i$ and $e_i$ are the observed and expected occurrences respectively.
💥 NOTE: all expected occurrences must be at least 5. 만약, 5 이하의 빈도를 가지는 카테고리가 있다면, 그것을 다른 카테고리에 합치는 pooling을 수행하라!
위의 예제에서는 카테고리가 단 2개인 상황이었다. 하지만, 주사위 굴리기와 같이 카테고리가 여러 개인 경우는 $\chi^2$ 분포의 DOF가 달라진다. 그 공식은 아래와 같다.
Definition. Degree of Freedom for Goodness-of-fit
The degree of freedom $\nu$ = (#. of categories after pooling - 1) - #. of parameters estimated
(#. of categories)에서 $-1$을 하는 이유는 Total value $n$이 주어졌기 때문이다. 마지막 카테고리의 값은 Deterministic하게 결정된다!
통계학에서의 DOF에 대해 궁금하다면, 아래의 포스트를 읽어보고 오자!
👉 Degree of Freedom in Statistics
Test for Independence
<Chi-squared goodness-of-fit Test>를 응용해 두 개의 카테고리가 서로 독립(independent)인지 검정해보자.
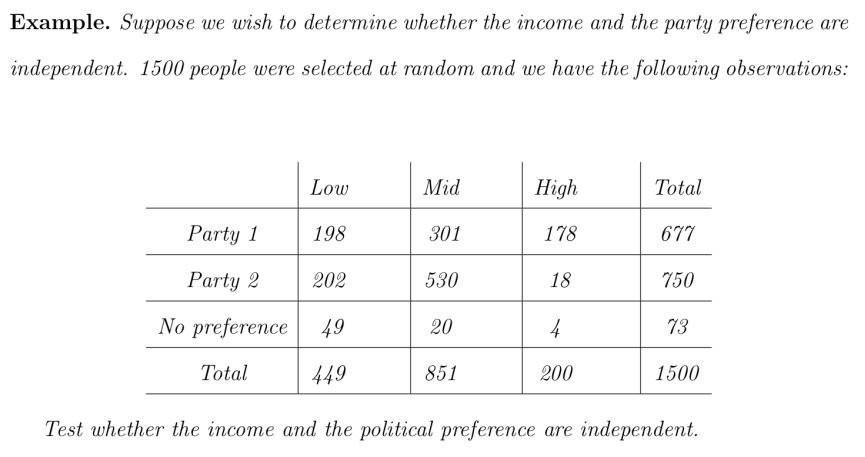
‘income’과 ‘political’이 서로 독립인지를 검정해보자. 아래와 같이 $H_0$와 $H_1$을 설정한다.
- $H_0$: income-political is independent
- $H_1$: they are not independent
$H_0$를 수식으로 표현하면 아래와 같다.
\[P(\text{party } 1 \; \And \; \text{low}) = P(\text{part } 1) \cdot P(\text{low})\]두 카테고리가 독립이라는 가정 $H_0$에서 유래한 위의 공식을 활용하면, 각 상황의 expected value $e_{ij}$를 얻을 수 있다.
예를 들어 $e_{11}$은
\[\begin{aligned} e_{11} &= 1500 \times P(\text{P1} \; \And \; \text{Low}) \\ &= 1500 \times \frac{677}{1500} \times \frac{499}{1500} \\ &= \frac{677 \cdot 499}{1500} = 225.21 \end{aligned}\]이런 방식으로 각 entry에 대한 expected value $e_{ij}$를 구한다.
다음으론 chi-square test의 공식에 $o_{ij}$, $e_{ij}$를 대입해 $\chi^2$-value를 구한다.
\[\chi^2 = \sum_{i=1}^3 \sum_{j=1}^3 \frac{(o_{ij} - e_{ij})^2}{e_{ij}}\]$\chi^2$ 분포의 DOF도 구해보면,
\[\begin{aligned} \nu &= (9-1) - \left((3-1) + (3-1)\right) \\ &= 8 - (2 + 2) = 4 \end{aligned}\]이때 “(#. of parameters estimated) = $4$”가 되는 이유는 다음과 같다.
우리가 ‘party’에 대한 parameter를 구하려면, 세 가지 경우에 대한 확률을 구해야 한다. 그런데, 확률의 경우 合이 1이 되기 때문에 세가지 경우 중 두 가지 경우만 구하면 된다. 따라서, ‘party’에 대해서 두 가지 parameter를 estimate 해야 하고, 마찬가지로 ‘income’에 대해서도 두 가지 parameter를 estimate 해야 한다. 따라서, (#. of parameters estimated)는 4개이다.
이것을 공식으로 작성하면 아래와 같다.
\[\begin{aligned} \nu &= r \cdot c - 1 - \left((r -1) + (c-1)\right) \\ &= r(c-1) - (c-1) \\ &= (r-1)(c-1) \end{aligned}\]$\chi^2$-value와 DOF $\nu$를 구했으면 검정을 수행하면 된다.
Reject $H_0$, if $\chi^2 > \chi^2_{\alpha} (\nu)$.
Test for Homogeneity
이번에는 <Goodness-of-fit Test>를 응용해 각 카테고리에서의 분포가 균일(homogeneous)한지 검정해보자. 예를 들면, “인종 별로 흡연자와 비흡연자 비율이 동일한가?”와 같은 질문을 검증하는 것이다.
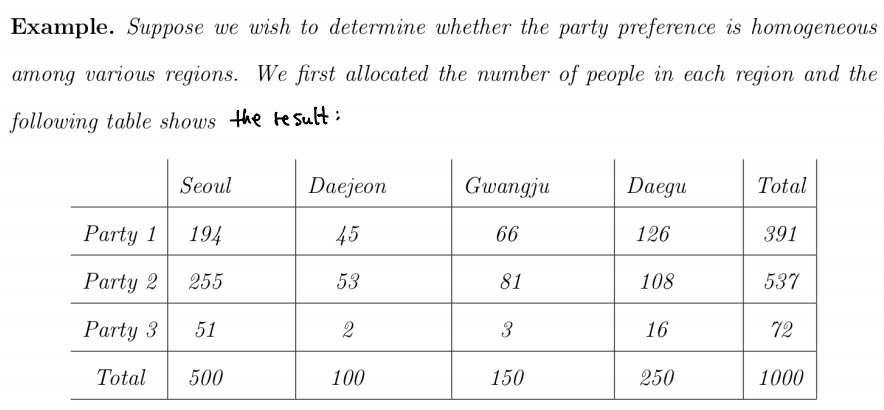
먼저 무엇을 검정하고자 하는지 명확히 정의해보자.
“Is the party preference homogeneous among various regions?”
이것을 확인하려면, ‘part $i$’을 선호하는 비율이 각 지역마다 모두 동일한지 확인해야 한다. 이것은 아래의 등식 성립함을 말한다.
\[P(\text{party } i \mid \text{Seoul}) = P(\text{part } i \mid \text{Daejeon}) = P(\text{party } i \mid \text{Gwangju}) = P(\text{party } i \mid \text{Daegu})\]이 등식을 null hypothesis $H_0$로 삼아 검정을 수행하자!
위의 표를 기준으로 $e_{11}$를 구해보자. 먼저 ‘Seoul’의 총 인구는 500이다. 그리고 전체 사람 수 중 ‘party 1’을 선호하는 사람의 비율은 391/1000이다. 따라서, $e_{11}$은
\[e_{11} = 500 \times \frac{391}{1000}\]마찬가지로 $e_{12}$의 경우는 $e_{12} = 100 \times 391 / 1000$로, $e_{21}$은 $e_{21} = 500 \times 537 / 1000$이다.
사실 Homogeneity Test는 앞에서 수행한 Independence Test와 동치이다. Homogeneity Test의 $H_0$가 Inpendence를 직접적으로 표현하진 않았지만, 약간 변형하면 Independence로 유도할 수 있다.
편의를 위해 $\text{party } i = B_i$, $\text{region } j = A_j$로 표시하겠다.
\[\begin{aligned} P(B_i \mid A_1) &= P(B_i \mid A_2) = x \\ \frac{P(B_i \cap A_1)}{P(A_1)} &= \frac{P(B_i \cap A_2)}{P(A_2)} = x \end{aligned}\]좌변의 분모를 우변으로 넘기면,
\[P(B_i \cap A_j) = x P(A_j)\]가 되는데, 이 $P(B_i \cap A_j)$를 전부 모으면 “Law of Total Probability”에 의해
\[P(B_i) = \sum_{j=1}^4 P(B_i \cap A_j) = x \cdot \cancelto{1}{\sum_{j=1}^4 P(A_j)} = x\]즉, $x = P(B_i)$이다. 이걸 처음의 수식에 대입하면,
\[P(B_i \mid A_1) = x = P(B_i)\]이것은 $B_i$와 $A_j$가 서로 독립임을 의미한다!!! $\blacksquare$
위의 증명을 통해 <Homogeneity Test>가 <Independence Test>와 동치임을 확인했다. 그래서 <Independence Test>에서 썼던 검정 방식을 그대로 쓰면 된다!!
DOF도 <Independence Test>의 공식으로 구해보면,
\[\nu = (r-1) (c-1) = (3 - 1) (4 - 1) = 6\]그리고 검정을 수행하면,
Reject $H_0$, if $\chi^2 > \chi^2_{\alpha}(\nu)$
Proportion Test and Chi-square Test
<chi-square test>가 “<proportion test>의 일반화”라는 걸 실제 값과 함께 다뤄보고자 한다.
One Proportion Case
앞면의 확률이 $p$인 p-coin이 있다. 아래의 가설을 검정하고자 한다.
- $H_0$: $p = 1/3$
- $H_1$: $p \ne 1/3$
$20$번의 실험으로 얻은 sample proportion은 $\hat{p} = 1/4$였다.
One Proportion Test의 Statistic은 아래와 같다.
\[\frac{p - \hat{p}}{\sqrt{p(1-p) / n}}\]이것에 대입해 z-value를 계산하면, $z = 0.791$이다. Alternative Hypothesis $H_1$ 이 양측 검정의 형태이므로 p-value를 구하면, $0.428$이다.
이번에는 chi-square GOF test를 해보자. Test Statistic은 아래와 같다.
\[\sum^2_{i=1} \frac{(o_i - e_i)^2}{e_i}\]이것에 대입해 $\chi^2$-value를 계산하면, $\chi^2 = 0.625$이다. DOF $\nu = 1$이므로 p-value를 구하면, $0.429$이다.
와우! 두 가지 접근 모두 동일한 p-value를 얻었다!!
Two Proportion Case
두 집합의 비율이 동일한지, $p_1 = p_2$인지를 검정하고자 한다. Test Statistic은 아래와 같다.
\[\frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\hat{p}\hat{q}(1/n_1 + 1/n_2)}}\]이때, $\hat{p}$은 pooled proportion이다.
\[\hat{p} = \frac{x_1 + x_2}{n_1 + n_2}\]z-value를 계산하기 위해 실험의 값을 임의의로 정해보면, $n_1 = 20$, $x_1 = 18$, $n_2 = 100$, $x_2 = 84$라고 해보자.
이것에 대입해 z-value를 계산하면, $z = 0.686$이다. 양측 검정에 대한 p-value를 구하면, $0.493$이다.
이번에는 <Homogeneity Test>로 접근해보자. Test Statistic은 아래와 같다.
\[\sum^2_{i=1} \sum^2_{j=1} \frac{(o_{ij} - e_{ij})^2}{e_{ij}}\]대입해서 $\chi^2$-value를 계산하면, $\chi^2 = 0.471$이다. 인터넷에 돌아다니는 Independent Test Calculator를 쓰면 금방 계산할 수 있다! DOF $\nu = 1$이므로 p-value를 구하면, $0.493$이다!
와우! 이번에도 두 가지 접근 모두 동일한 p-value를 얻었다!
맺음말
검정(Testing)에 대한 내용은 여기까지다!! 👏 이것으로 “통계학(Statistics)”의 기본적인 내용을 모두 살펴본 것이다!! 😆
다음 포스트부터 <Simple Linear Regression>이라는 새로운 챕터를 살펴본다. 주어진 데이터에서 “Linear Regression”의 계수 $\beta_i$들을 어떻게 찾을 수 있을지를 다루는 챕터다!
👉 Introduction to Linear Regression
