Longest Path, Subset Sum
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Longest Path Problem
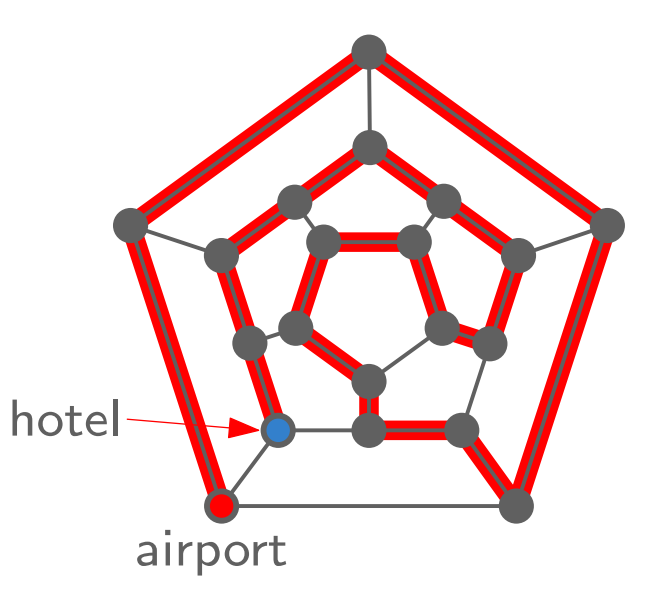
<Shortest Path Problem>은 다익스트라 알고리즘으로 효율적으로 해결할 수 있음을 알고 있다. 그렇다면 <Longest Path Problem>은 어떨까? 당신이 택시 기사라면, 출발지에서 목적지까지 최대한 긴 경로로 운전해서 최대의 택시비를 벌고 싶을 것이다. (단, 왔던 길을 뱅뱅 도는 얕은 수법을 쓴다면 똑독한 승객이 눈치 챌 테니, 왔던 길은 다시 가지 않아야 할 것이다.) 그래서 <Longest Path Problem>을 <Taxicab Rip-off> 문제, 즉 ‘택시 바가지’ 문제라고도 부른다.
Problem. Longest Path Problem
Given a graph with non-negative edge weights and two vertices $s$ and $t$, along with a goal $g$, find a simple path from $s$ to $t$ with total weight at least $g$.
Subset Sum Problem
<Knapsack Problem>을 기억하는가? 배당의 용량 $W$와 물건들 $(w_i, v_i)$가 있을 때 용량을 넘기지 않으면서 최대한의 가치를 담는 문제였다. 그러나 이번에는 정확히 용량 $W$ 만큼 물건을 담아서 최대한의 가치를 담으려 한다면 어떨까? <Knapsack Problem> 문제의 변형인 이 문제는 <Subset Problem>라는 이름의 문제로 주어진 집합의 부분집합(subset)을 선택해 원하는 용량 $W$와 동일한 값을 갖도록 하는 문제다.
Problem. Subset Sum Problem
Given a set of integers and a value $W$, find a subset of integers that adds up to exactly $W$.
<Knapsack Problem>이 $O(nW)$의 시간 복잡도로 효율적으로 해결되는 반면, <Subset Problem>에 대해서는 polynomial algorithm이 존재하지 않으며, 가능한 subset 조합을 일일이 찾는 수 밖에 없다. “P and NP” 포스트에서 NP 문제의 예시로 들었던 “원소 합이 0이 되는 부분집합” 문제가 바로 이 <Subset Problem>에 속한다!
이것으로 정규 수업에서 소개한 대표적인 NP 문제들을 가볍게 살펴보았다. 이제 NP 문제들이 어떻게 환원(reduction) 되는지 하나씩 살펴보겠다.