Reduction (2)
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
3-SAT → Independent-Set
Claim. 3-SAT $\le_P$ Independent-Set
우리는 아래와 같은 3-SAT 문제를 Independent-Set 문제로 환원(Reduction)할 것이다.
\[(\bar{x} \lor y \lor \bar{z})(x \lor \bar{y} \lor z)(x \lor y \lor z)(\bar{x} \lor \bar{y})\]이때, Indenpendent-Set 문제 $(G, k)$는 $k$개의 pairwise non-adjacent vertices를 찾는 문제가 된다. 위의 3-SAT 문제는 총 4개의 clauses가 존재하는데, 이 경우 Reduction으로 만들어진 Independent-Set 문제는 $(G, 4)$으로 $k=4$이 된다.
Proof
Given an instance $\Phi$ of 3-SAT with $k$ clauses, we construct an instance $(G, k)$ of Indenpendent-Set that has an indenpendent set of size $k$ iff $\Phi$ is satisfiable.
[Problem Transformation]
Construct an instance of Independent-Set from an instance of 3-SAT as following rule:
1. $G$ contains 3 vertices for each clause, one for each literal.
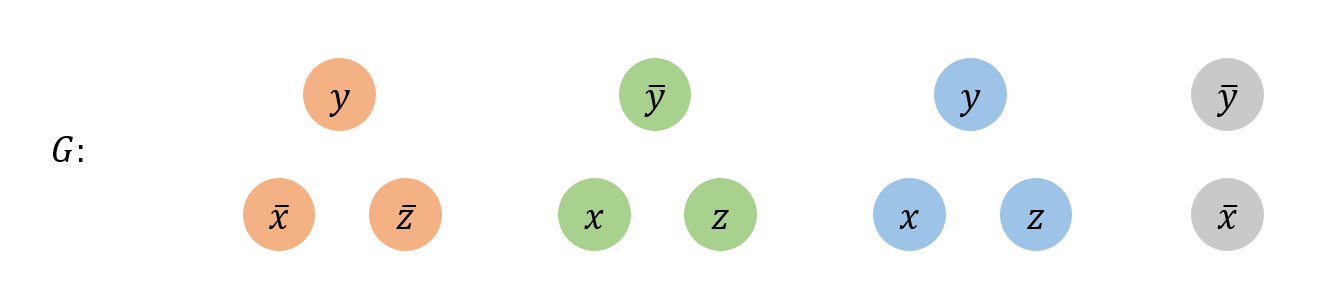
2. Connect 3 literals in a clause in a triangle.
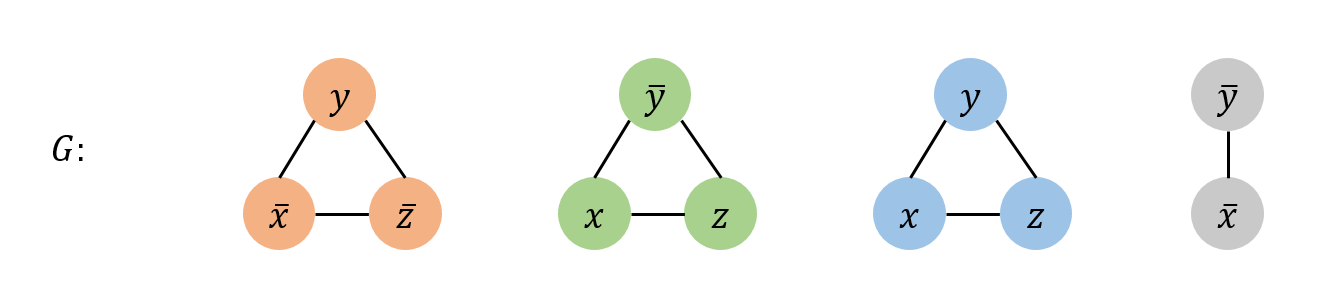
3. Connect literal to each of its negations.
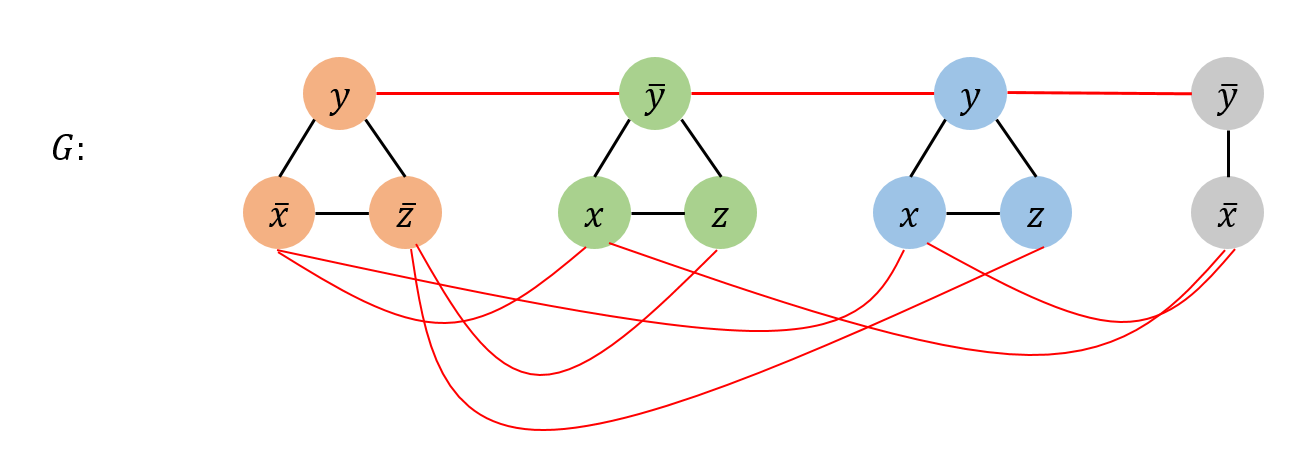
[Solution Transformation]
(1) Given an independent set $S$ of $k$ vertices in $G$, it is possible to efficiently recover a satisfying truth assignment to $\Phi$.
For any variable $x$, the set $S$ cannot contain vertices labeled both $x$ and $\bar{x}$, because any such pair of vertices is connected by an edge (step 3). So assign $x$ a value of $\text{true}$ if $S$ contains a vertex labeled $x$, and a value of $\text{false}$ if $S$ contains a vertex labeled $\bar{x}$. If $S$ contains neither $x$ or $\bar{x}$, then assign any value to $x$. Since $S$ has $k$ vertices, it must have one vertex per clause (step 2). This truth assignment guarantees to satisfy all clauses.
(2) If graph $G$ has no independent set of size $k$, then 3-SAT instance $\Phi$ is unsatisfiable.
Contrapositive(대우)를 통해 증명한다. “If $\Phi$ has a satisfying assignment, then $G$ has an independent set of size $k$.” $\Phi$가 satisfiable이므로, 각 clause에서 적어도 하나의 literal은 $\text{true}$이다. 각 literal에서 $\text{true}$인 literal을 하나씩 선택하면, 총 $k$개의 literal을 선택할 수 있고, 이것이 곧 size $k$인 independent set $S$이다.
Independent-Set → Vertex Cover
사실 이 부분은 Independent Set, Vertex Cover, and Clique 포스트에서 이미 다루었다. 그러나 상기도 할 겸 일부만 다시 한번 살펴보자.
\[\text{Vertex Cover} \equiv_P \text{Independent Set}\]There is very fun fact: “If $S$ is a vertex cover, then $V \setminus S$ is an independent set.”
$V \setminus S$가 independent set이 아니라고 하자, 그러면 어떤 $x, y \in V \setminus S$에 대해 edge가 존재함을 의미한다. 그러나 $x, y$ 모두 $V \setminus S$에 속하기 때문에 $x, y$를 잇는 edge는 Vertex Cover $S$에 의해 커버되지 않는다. 이것은 $S$가 Vertex Cover라는 사실에 모순이다. 따라서, $S$가 Vertex Cover라면, $V \setminus S$는 Independent Set이다.
Independent-Set → Clique
이 부분도 Independent Set, Vertex Cover, and Clique 포스트에서 이미 다루었다.
For a graph $G = (V, E)$, define the complement graph $\bar{G} = (V, \bar{E})$. Then, an independent set $S$ of $G$ is a clique of $\bar{G}$.
$G$에 대한 Indenpendent-Set을 찾고 싶다면, complement graph $\bar{G}$ 위에서 Clique를 찾으면 되었다. 반대의 경우도 마찬가지다.
3-SAT → Clique
Claim. 3-SAT $\le_P$ Clique
이번에는 아래와 같은 3-SAT 문제를 Clique 문제로 환원해보자.
\[(\bar{x} \lor y \lor z)(x \lor \bar{y} \lor z)(\bar{x} \lor y \lor w)\]Proof
Given an instance $\Phi$ of 3-SAT consisting of $k$ clauses, we construct an instance $(G, k)$ of Clique that has a clique of size $k$ iff $\Phi$ is satisfiable.
[Problem Transformation]
Construct an instance of Clique from an instance of 3-SAT as following rule:
1. $G$ contains 3 vertices for each clause, one for each literal.
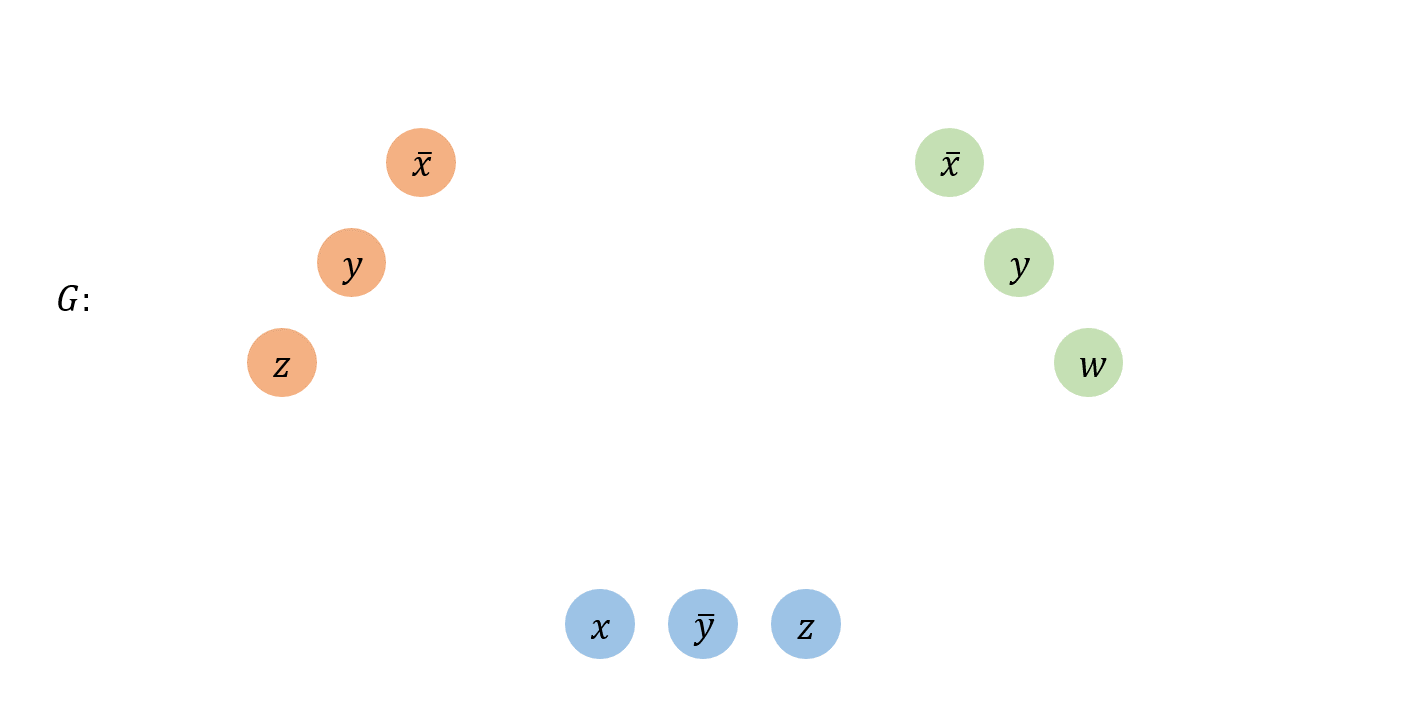
2. Connect a literal $u$ to other literal $v$ if they belong to different clauses and $u \ne \bar{v}$.
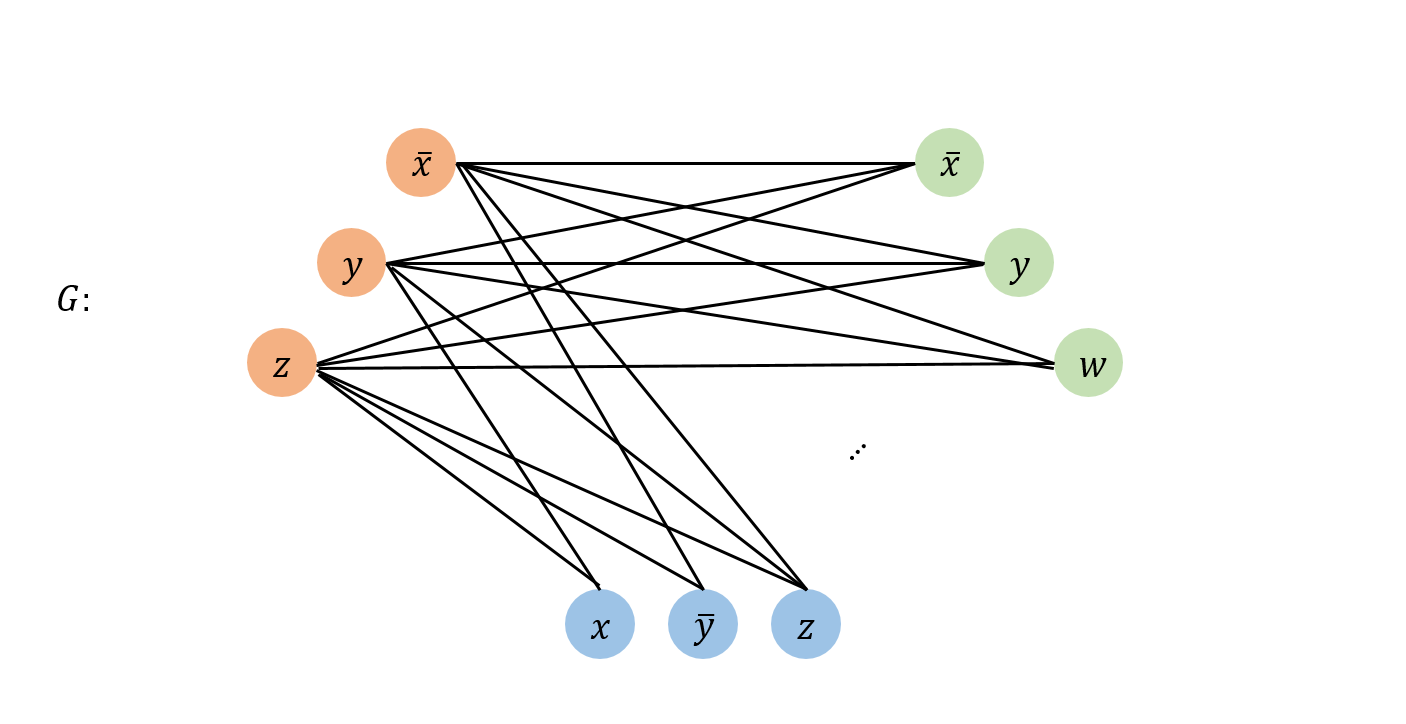
이제 구성한 $(G, k)$ 위에서 $k$-clique를 찾으면 된다. 위 문제의 경우, 3-clique를 찾으면 되는데, $\bar{x}$, $\bar{x}$, $z$를 선택해서 아주 쉽게 찾을 수 있다.
앞에서 Independent-Set 문제를 Clique 문제로 환원할 수 있다고 했다. 두 문제의 관계는 complement $G \leftrightarrow \bar{G}$의 관계 였다. 이번 3-SAT $\le_P$ Clique 문제도 비슷해보이지 않는가? Clique 그래프 $(G, k)$의 Complement $(\bar{G}, k)$를 구한 후 Independent-Set을 구해도 동일하게 3-SAT 문제의 해답을 찾을 수 있다.
