Application of Derivatives: Problem Solving

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 공부하면서 재밌어 보였던 문제들과 풀이들을 모아서 정리한 포스트 입니다. 미적분학 포스트 전체 보기

Geometric Mean

The geometric mean of two positive numbers $a$ and $b$ is the number $\sqrt{ab}$. Show that the value of $c$ in the conclusion of the Mean Value Theorem fro $f(x) = 1/x$ on an interval of positive numbers $[a, b]$ is $c = \sqrt{ab}$.

MVT를 충실히 적용하면 되는 문제.

By MVT, there exist some $c$ on $[a, b]$ s.t. $f’(c) = \dfrac{f(b) - f(a)}{b-a}$.

\[f'(c) = \frac{1/b - 1/a}{b - a} = -ab\]

이때, $f’(x) = - 1 / x^2$이므로 $c = \sqrt{ab}$가 된다. $\blacksquare$

기하 평균은 왜 기하라고 부르는가?

지금까지 살면서 “기하 평균”를 꽤 몇번 마주쳤는데 이번에 문제를 풀면서 문득 왜 이걸 “기하” 평균이라고 부르는지 궁금해졌다.

Quora - Why is “geometric mean” called geometric?에서 만족할만한 답변을 찾았다 ㅎㅎ 그리고 정말 기하학에서 유래한 것이 맞다!!

직사각형의 각 변이 $a$, $b$ 일때, 그 직사각형의 넓이는 $ab$이다. 그런데 그 직사각형이랑 정확히 똑같은 넓이를 갖는 정사각형의 한 변의 길이 $x$를 구하기 위해 $x^2 = ab$로 뒀고, 이때의 $x$ 값인 $x = \sqrt{ab}$를 기하 평균으로 둔다고 한다.

요걸 정육면체, 그 이상의 차원으로도 기하 평균을 확장할 수 있다.

그럼 조화 평균은 왜 조화 평균인가?

갑자기 “조화 평균”은 왜 그럴까…라는 생각도 하게 되었다 ㅋㅋㅋ

Harmonic Mean.

\[\left(\frac{1/a + 1/b}{2}\right)^{-1} = \frac{2ab}{a+b}\]

요건 $\{ 1, 1/3, 1/5, 1/7, … \}$와 같이 역수가 등차수열을 이루는 “조화 수열”에서 수열의 연속한 세 값 $a$, $b$, $c$에서 $b$의 값을 조화 중항 또는 조화 평균이라고 한다.

이때 $b$와 $a$, $c$의 값으로 표현하면 조화 평균과 같은 형태가 유도된다.

Cauchy’s Mean Value Theorem

Suppose functions $f$ and $g$ are continuous on $[a, b]$ and differentiable throughout $(a, b)$ and also suppose $g’(x) \ne 0$ throughout $(a, b)$. Then there exists a number $c$ in $(a, b)$ at which

\[\frac{f'(c)}{g'(c)} = \frac{f(b) - f(a)}{g(b) - g(a)}\]

일단 코시의 정리가 어떤 의미를 가지는지부터 이해해보자. 함수 $f$와 $g$가 각각 parametric function의 $y$, $x$를 표현하는 함수라고 해보자. (참고로 Parametric Function은 미적2 내용이다.)

\[\begin{aligned} x &= g(t) \\ y &= f(t) \end{aligned}\]

이때, $t=a$와 $t=b$에 대한 평균 변화율을 구하면 아래와 같을 것이다.

\[\text{slope} = \frac{f(b) - f(a)}{g(b) - g(a)}\]

그런데 코시의 정리는 이 slope의 기울기와 동일한 기울기를 가진 접선이 $t: (a, b)$ 범위 안의 어떤 $t=c$에 존재함을 말한다.

즉,

\[\frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{f'(c)}{g'(c)} = \frac{f(b) - f(a)}{g(b) - g(a)}\]

인 시점 $t=c$를 찾을 수 있다는 것이다.

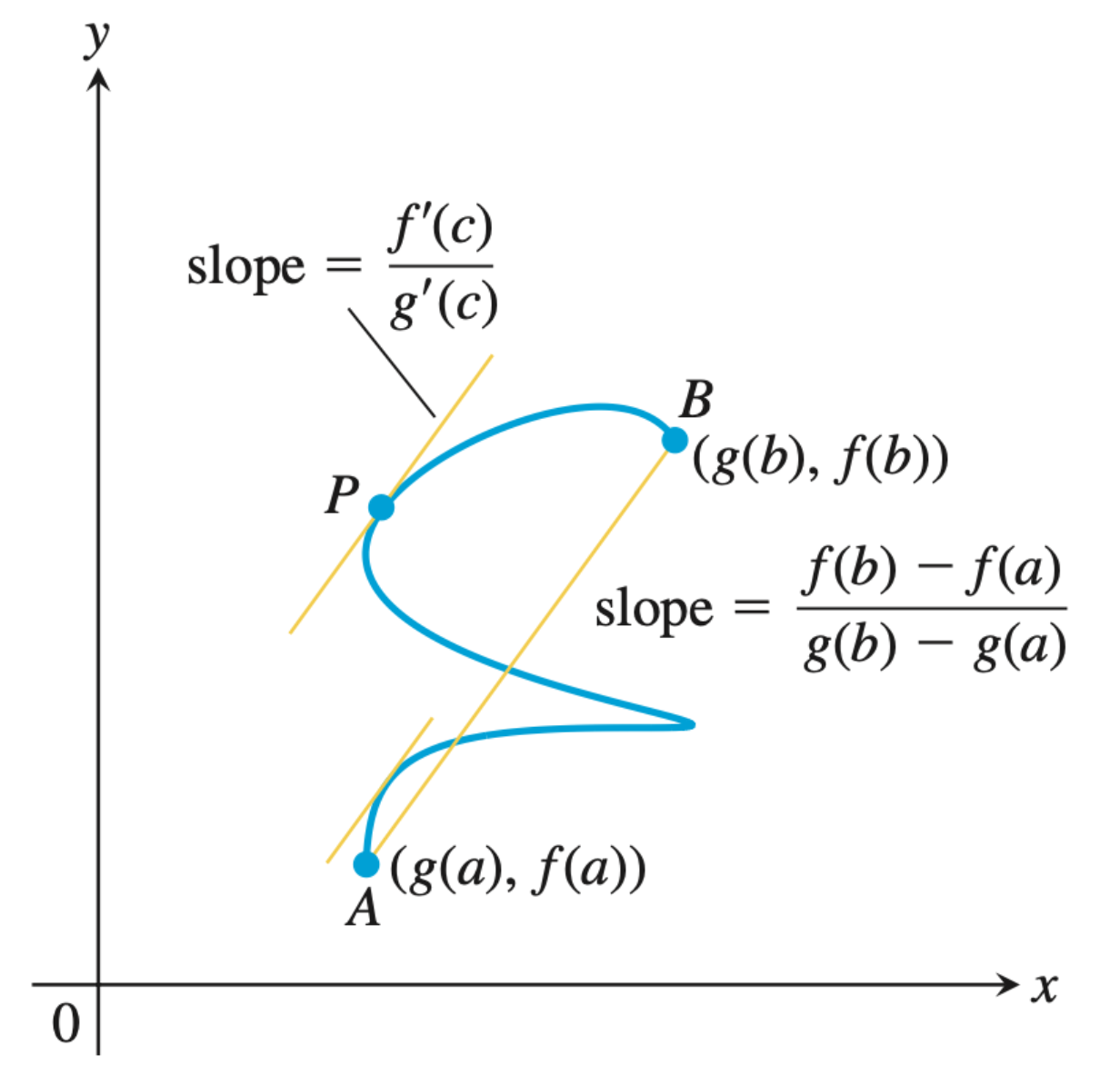
요걸 시각적으로 확인하면 이런 느낌이다.

증명은 MVT를 활용하면 되는데, 간단한 것 같아서 패스…!

Proof of l’hôpital’s rule

일단 증명을 하기 전에 상황부터 세팅하자.

Let assume, $f(a) = g(a) = 0$, and $g’(a) \ne 0$. Then,

\[\lim_{x \rightarrow a} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}\]

일단 $\lim_{x \rightarrow a} \frac{f(x)}{g(x)}$는 $0/0$ 꼴의 부정형인 상황이다.

함숫값의 극한을 0으로 보내는 $a$라는 값의 오른쪽에서 $a$로 접근하는 $x \rightarrow a^{+}$ 상황을 살펴보자. 반대인 $x \rightarrow x^{-}$ 상황은 대칭이라서 생략한다.

그려면 코시의 정리에 따라 $(a, x)$ 사이에 아래 식을 만족하는 $c$가 존재함이 보장된단.

\[\frac{f'(c)}{g'(c)} = \frac{f(x) - f(a)}{g(x) - g(a)}\]

이때, $f(a) = g(a) = 0$이므로

\[\frac{f'(c)}{g'(c)} = \frac{f(x)}{g(x)}\]

이제 양쪽에 극한을 취하면

\[\lim_{x \rightarrow a^{+}} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a^{+}} \frac{f'(c)}{g'(c)}\]

에서 $x \rightarrow a^{+}$가 되면, $(a, x)$ 사이에 있는 $c$는 $c \rightarrow a$가 된다. 따라서

\[\lim_{x \rightarrow a^{+}} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a^{+}} \frac{f'(c)}{g'(c)} = \lim_{x \rightarrow a^{+}} \frac{f'(a)}{g'(a)}\]

$\blacksquare$

Variation of Sine Function

$(\sin x)^x$

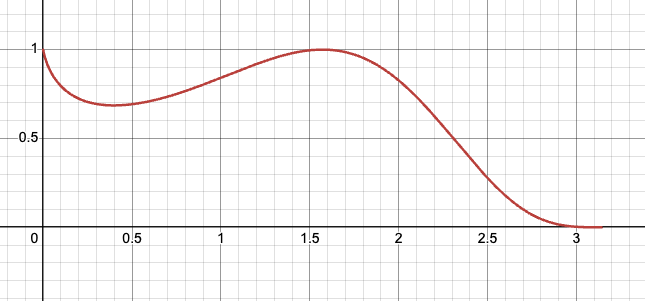
연습 문제에 나왔던 함수다. 일단 문제에서는 그래프의 개형을 그려보고, 함수가 $x=0$에서 연속이기 위해 가져야 할 함숫값에 대해서 물어봤다.

$x=0$에서는 $0^0$ 꼴이 되는데, Ch 1: Limit and Continuity에서도 봤듯이 $0^0$의 극한의 값은 $1$로 할당 했었다. 실제로 함수 그래프도 $x = 0$에서 $1$의 값을 가진다!

물론 $0^0$의 극한이 $1$이었으니 $(\sin x)^x$의 극한도 $1$이 되어야 한다는 건 엄밀한 증명이 아니다. 엄밀히 증명하기 위해서 power form의 부정형에 대한 극한을 확인하면 된다. (그리고 이때 로피탈을 쓰게 된다.)

Let $f(x) = (\sin x)^x$, we will find the limit of $\ln f(x)$.

\[\lim_{x \rightarrow 0} \ln f(x) = \lim_{x \rightarrow 0} x \cdot \ln \sin x = \lim_{x \rightarrow 0} \frac{\ln \sin x}{1/x}\]

이제 $0/0$ 꼴의 극한이니 로피탈 정리를 적용하면 된다 ㅎㅎ

\[\lim_{x \rightarrow 0} \frac{\ln \sin x}{1/x} \Rightarrow \lim_{x \rightarrow 0} \frac{\cos x/\sin x}{- 1/x^2} = \lim_{x \rightarrow 0} \frac{x}{\sin x} \cdot (- \cos x \cdot x) = 0\]

$\ln f(x)$의 극한이 $0$이므로 $f(x)$의 극한은 $1$이 된다! $\blacksquare$

$(\sin x)^{\tan x}$

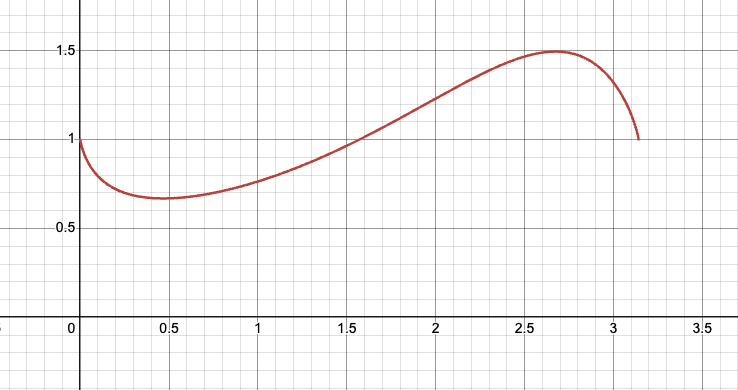
$(\sin x)^x$와 비슷하지만 이번에는 지수가 $\tan x$가 되었다!

본래 $\tan x$가 $x = \pi/2$ 지점에서 정의가 되지 않는다. 그러나 위의 함수는 해당 지점에서 값이 정의된다!! 어떻게 된 걸까!!

일단 $\sin x$가 $x = \pi/2$에서 $1$이기 때문에 이번에는 $1^{\infty}$의 상황이다! 물론 $x = 0$에서도 연속성을 위한 확장이 필요하긴 하다.

이번에도 power form의 부정형 극한을 핸들링 하는 접근을 적용하면 된다.

We will find the limit of $\ln f(x)$

\[\lim_{x \rightarrow 0} \ln f(x) = \lim_{x \rightarrow 0} \tan x \cdot \ln \sin x = \lim_{x \rightarrow 0} \frac{\ln \sin x}{1/\tan x}\]

이제 극한을 찾기 위해 미분하자. 로피탈의 정리를 쓴다.

\[\lim_{x \rightarrow 0} \frac{\ln \sin x}{1/\tan x} = \lim_{x \rightarrow 0} \frac{\cos x / \sin x}{- \sec^2 x / \tan^2 x} = \lim_{x \rightarrow 0} \frac{\cos^3 x}{\sin x} \cdot \tan^2 x = \lim_{x \rightarrow 0} \cos x \cdot \sin x = 0\]

$\ln f(x)$의 극한값이 $0$이므로 $f(x)$의 극한값은 $1$이 된다. $\blacksquare$