Vector Form of Green Theorem

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

들어가며

발산과 회전에 대해서 배웠다면, 그린 정리를 이 둘을 사용해 표현할 수 있습니다!

Vector form of Green’s Theorem

그린 정리(Green’s Theorem)는 2차원 평면 위의 벡터장 $\mathbf{F}(x, y)$에 대한 선적분이 그것의 성분 벡터의 편미분을 조합한 어떤 이중 적분과 연결하는 정리였다.

[그린 정리]

\[\int_C \mathbf{F} \cdot d\mathbf{r} = \int_C P \, dx + Q \, dy = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA\]

그런데 이 정리를 3차원 공간에서 $z$ 좌표가 0인 3차원 벡터장 $\mathbf{F}(x, y, 0)$으로 바꾸어 살펴보면, 그린 정리를 발산(div)과 회전(curl)과 연결 해볼 수 있다. 😮

내용을 정리하기 전에 dimenchoi님의 그린 정리의 직관적인 이해와 증명(Green’s Theorem) 포스트가 이 부분을 이해하는데 많은 도움이 되었음을 밝힌다. 아래 글을 읽기 전에 위의 포스트를 먼저 읽고 오길 강추 한다!!

Tangential Form

2차원의 벡터장에 $z=0$인 $z$ 성분을 추가하여 3차원 벡터장 $\mathbf{F} = \left< x, y, 0\right>$을 생각해보자. 이때, 이 벡터장의 curl 벡터는 아래와 같다.

\[\text{curl } \mathbf{F} = \left|\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P(x, y) & Q(x, y) & 0 \end{matrix}\right| = \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \mathbf{k}\]

요기에 $z$ 성분만 있는 벡터에 unit vector $\mathbf{k}$를 내적하면, 익숙한 식이 나온다.

\[(\text{curl } \mathbf{F}) \cdot \mathbf{k} = \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\]

요건 그린 정리에서 이중 적분에 들어가는 아주 익숙한 형태다!! 그래서 식을 정리하면…

\[\int_C \mathbf{F} \cdot d\mathbf{r} = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA = \iint_D \left( \text{curl } \mathbf{F} \right) \cdot \mathbf{k} \, dA\]

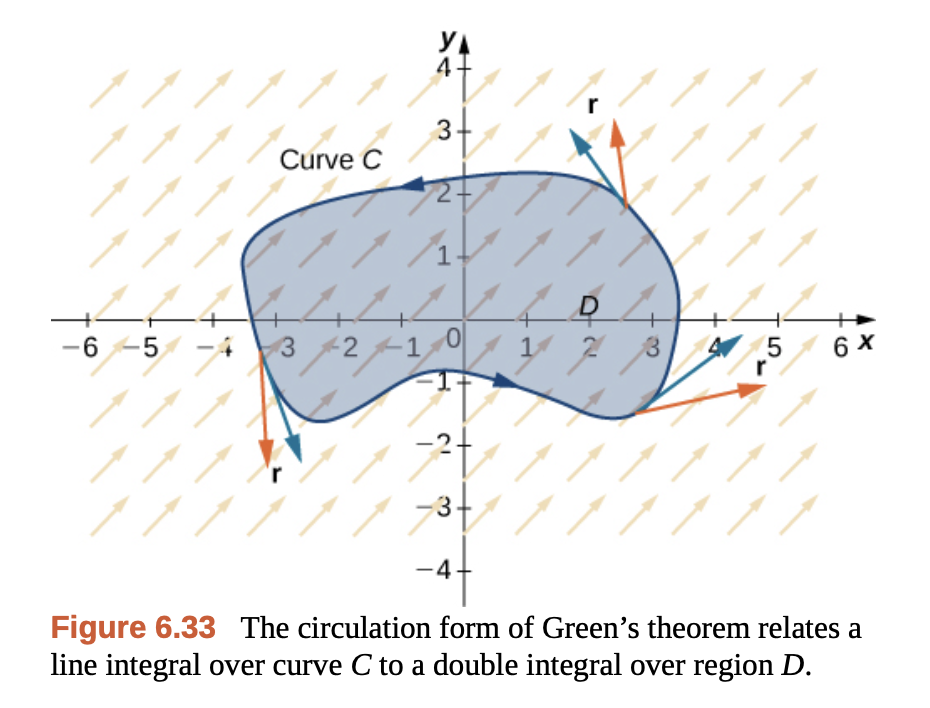Gilbert Strang - Calculus Vol 3.

Tangential Form은 영역 $D$ 내부에서의 회전(curl)의 총합이 경계 곡선 $C$ 위에서의 tangential integral로 대신 구할 수 있음을 말하는 것이다.

Normal Form

그린 정리의 Normal Form은 선적분을 곡선의 진행 방향 $d\mathbf{r}$과 수직인 벡터에 대해서 선적분을 수행하는 것이다.

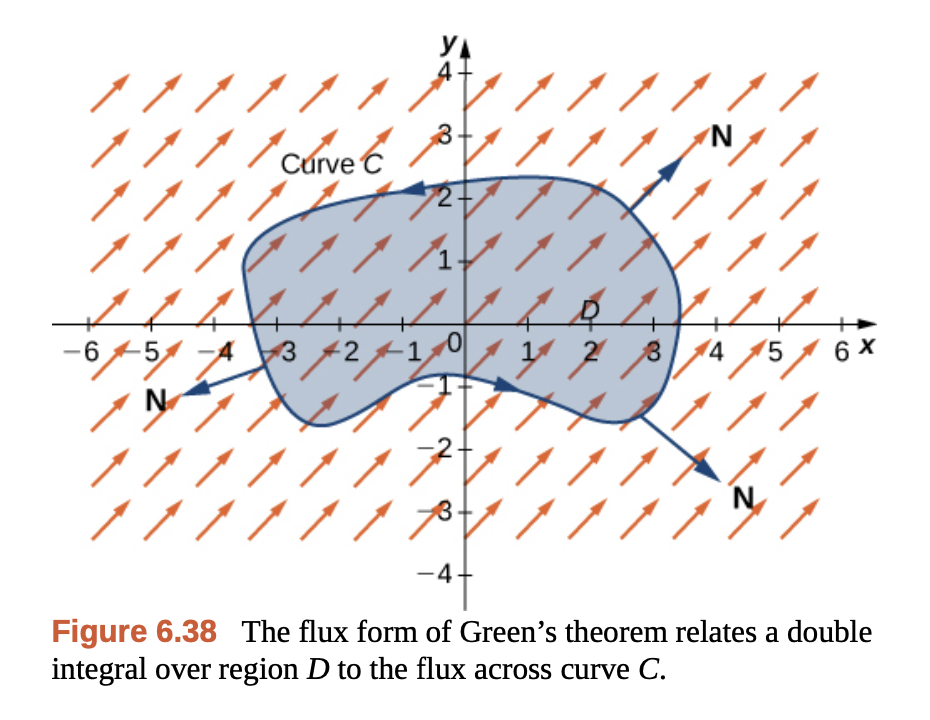Gilbert Strang - Calculus Vol 3.

\[\oint_C \mathbf{F} \cdot \mathbf{N} \, ds\]

그리고 이것은 곡선 $C$가 만드는 영역 $D$를 출입하는 유체의 흐름인 발산(divergence)의 총합의 값과 동일하다.

\[\oint_C \mathbf{F} \cdot \mathbf{N} \, ds = \iint_D \left( \nabla \cdot \mathbf{F} \right) \, dA = \iint_D \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \right) \, dA\]

위의 식이 어떻게 유도되는지를 좀더 살펴보자.

먼저, 곡선 $C$가 아래와 같은 벡터 매개방정식이라고 생각해보자.

\[\mathbf{r}(t) = x(t) \, \mathbf{i} + y(t) \, \mathbf{j}\]

이때, 곡선에 접하는 Unit Tangent Vector $\mathbf{T}(t)$를 구하면 아래와 같다.

\[\mathbf{T}(t) = \frac{x'(t)}{\left| \mathbf{r}'(t) \right|} \, \mathbf{i} + \frac{y'(t)}{\left| \mathbf{r}'(t) \right|} \, \mathbf{j}\]

그리고 이에 대한 노멀 벡터 $\mathbf{N}(t)$는 $\mathbf{T}(t) \cdot \mathbf{N}(t) = 0$임을 생각하면 아래와 같이 유도된다.

\[\mathbf{N}(t) = \frac{y'(t)}{\left| \mathbf{r}'(t) \right|} \, \mathbf{i} - \frac{x'(t)}{\left| \mathbf{r}'(t) \right|} \, \mathbf{j}\]

이제 다시 적분식으로 돌아오자. 적분식에서 미소길이량을 곡선의 매개 변수로 다시 쓰면 아래와 같다.

\[\oint_C \mathbf{F} \cdot \mathbf{N} \, ds = \oint_C (\mathbf{F} \cdot \mathbf{N}) (t) \, \left| \mathbf{r}'(t) \right| \, dt\]

그리고 이 식을 잘 정리하면…

\[\begin{aligned} \oint_C \mathbf{F} \cdot \mathbf{N} \, ds &= \oint_C (\mathbf{F} \cdot \mathbf{N}) (t) \, \left| \mathbf{r}'(t) \right| \, dt \\ &= \oint_C \left( \frac{P(x, y) \cdot y'(t)}{\left| \mathbf{r}'(t) \right|} - \frac{Q(x, y) \cdot x'(t)}{\left| \mathbf{r}'(t) \right|} \right) \, \left| \mathbf{r}'(t) \right| \, dt \\ &= \oint_C P(x, y) \cdot y'(t) \, dt - Q(x, y) \cdot x'(t) \, dt \\ &= \oint_C P \, dy - Q \, dx \end{aligned}\]

마지막 식을 $dx$, $dy$ 순서를 다시 맞추고, 그린 정리의 형식에 맞춰 편미분으로 다시 쓰면 아래와 같다.

\[\begin{aligned} &\oint_C P \, dy - Q \, dx \\ &= \oint_C \left( - Q \, dx + P \, dy \right) \\ &= \iint_D \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \right) \, dA \end{aligned}\]

그리고 위의 마지막 식은 벡터장 $\mathbf{F}$에 발산(div) 연산을 취한 $\text{div } \mathbf{F} = \nabla \cdot \mathbf{F}$와 같다.

$\blacksquare$

맺음말

저는 처음에 그린 정리를 2가지 형태로 포함할 수 있다는 사실을 받아들이는게 힘들었습니다.

Tangential Form은 나중에 스토스크 정리가 되고, Normal Form은 나중에 발산 정리가 됩니다.