Stokes’ Theorem
복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기
이번 챕터는 Joel Feldman - CLP Calculus 교재의 도움을 많이 받았다.
Stokes’ Theorem
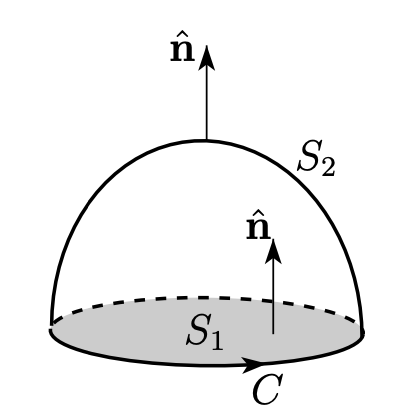
그린 정리는 “2차원 평면 $S_1$”에서의 이중 적분이, 평면의 경계를 이루는 곡선에 대한 선적분과 관련 있다고 얘기 했다.
스토크스 정리는 “3차원 곡면 $S_2$”에서의 이중 적분이, 곡면의 경계를 이루는 곡선에 대한 선적분과 관련 있다고 얘기한다.
즉, 그린 정리와 스토스크 정리 둘다 평면/곡면에 대한 적분을 경계 곡선에 대한 선적분으로 해석할 수 있다는 것으로 말한다.
[스토크스 정리]
\[\iint_{S_2} \text{curl } \mathbf{F} \cdot d\mathbf{S} = \int_{C} \mathbf{F} \cdot d \mathbf{r}\]이때, 곡선 $C$를 경계 곡선으로 갖는 곡면/평면은 여러 개가 있을 수 있는데, 스토스크 정리에 따라 그들의 curl 적분값 모두 같은 값을 가지게 된다.
[by 스토크스 정리]
\[\iint_{S_2} \text{curl } \mathbf{F} \cdot d\mathbf{S} = \iint_{S_1} \text{curl } \mathbf{F} \cdot d\mathbf{S}\]due to having save boundary curve $C$.
그래서 적분이 어렵다면, 같은 경계를 갖는 더 쉬운 곡면으로 바꾸어 곡면에 대한 curl 적분을 수행할 수도 있다고 한다.
닫힌 곡면에 대해
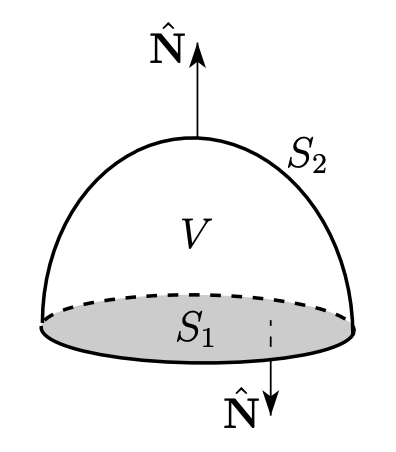
이번에는 $S_2$가 윗뚜껑이고, $S_1$이 아랫뚜껑인 닫힌 곡면에서의 곡면의 curl 적분을 생각해보자. 닫힌 곡면의 방향은 항상 바깥 방향(outward)로 향하기 때문에 아랫뚜껑 $S_1$는 아래 방향을 바라본다.
이 닫힌 곡면에 대해 곡면 curl 적분을 해보자. 곡면이 $S_1$, $S_2$로 분할 되고, 둘의 Surface Orientation이 반대 방향이므로,
\[\iint_{S_2} \text{curl } \mathbf{F} \cdot d\mathbf{S} - \iint_{S_1} \text{curl } \mathbf{F} \cdot d\mathbf{S}\]가 되고, 스토스크 정리에 의해 두 면적분의 경계 곡선의 선적분으로 바꿔보면,
\[\int_{C} \mathbf{F} \cdot d \mathbf{r} - \int_{C} \mathbf{F} \cdot d \mathbf{r} = 0\]이 된다. 즉, 결과를 일반화 하면 “닫힌 곡면에서 curl 벡터에 대한 곡면 적분의 값은 모두 0이 된다”라고 말할 수 있다.
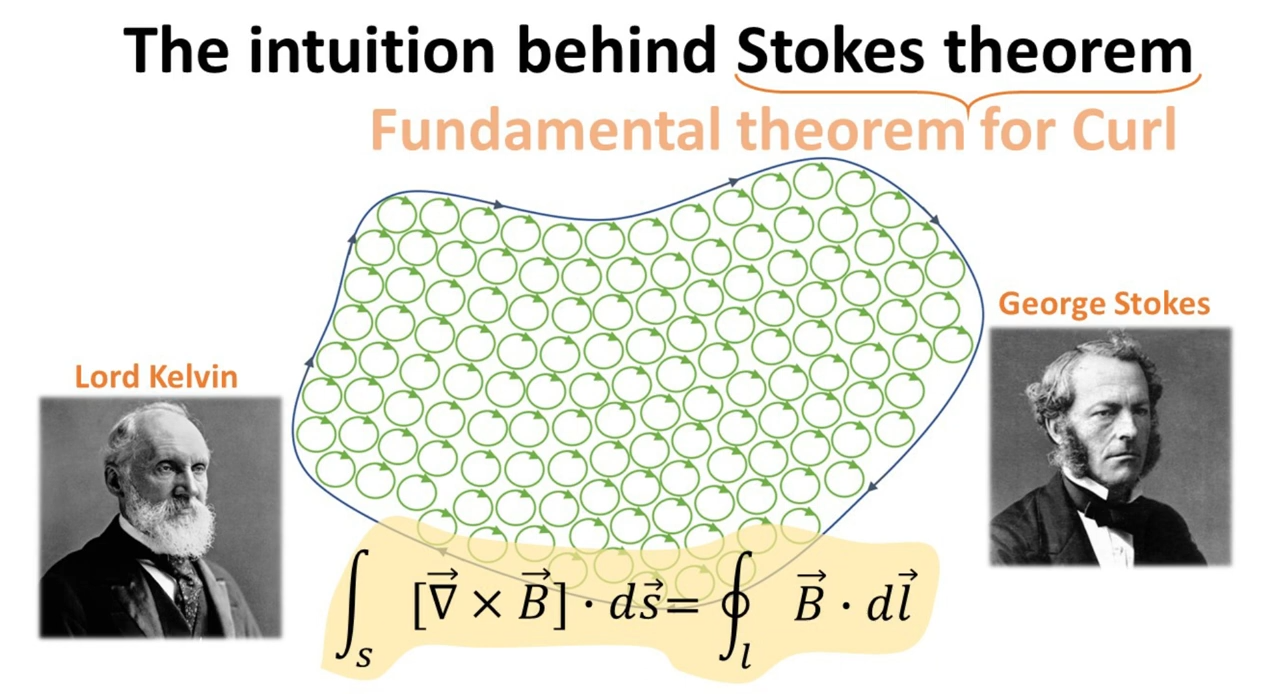Youtube: The intuition behind Stokes Curl theorem
스토크스 정리를 공부하면서 항상 헷갈렸던 이유는, 명제가 모든 벡터장에서 성립하는게 아니라 오직 curl 벡터장 $\nabla \times \mathbf{F}$에 대해서만 성립한다는 사실을 인지하지 못 했기 때문인 것 같다. curl 벡터의 경우 미소 영역에서 회전이 인접한 곳의 회전과 상쇄된다는 성질이, 곡면의 적분이 경계에서의 선적분과 같다는 것도 말하고, 닫힌 곡면에서의 면적분이 “0”라는 결과도 유도한다.
발산 정리 맛보기
위의 닫힌 곡면의 예제에서 발산 정리를 슬쩍 유도할 수 있다. 발산 정리도 경계에 대한 적분의 성질로, 부피 $V$에 대한 적분과 부피의 경계 곡면 $\partial V$에 대한 적분이 같다는 걸 말하는 정리다.
[curl 벡터의 면적분을 부피 적분으로 해석 by 발산 정리]
\[\iint_{\partial V} \nabla \times \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot (\nabla \times \mathbf{F}) \, dV\]이때, $\nabla \cdot (\nabla \times \mathbf{F}) = 0$라는 항등식에 의해 부피 적분의 값이 0이 되고, 덩달아 curl 벡터의 면적분 값도 0이 된다.