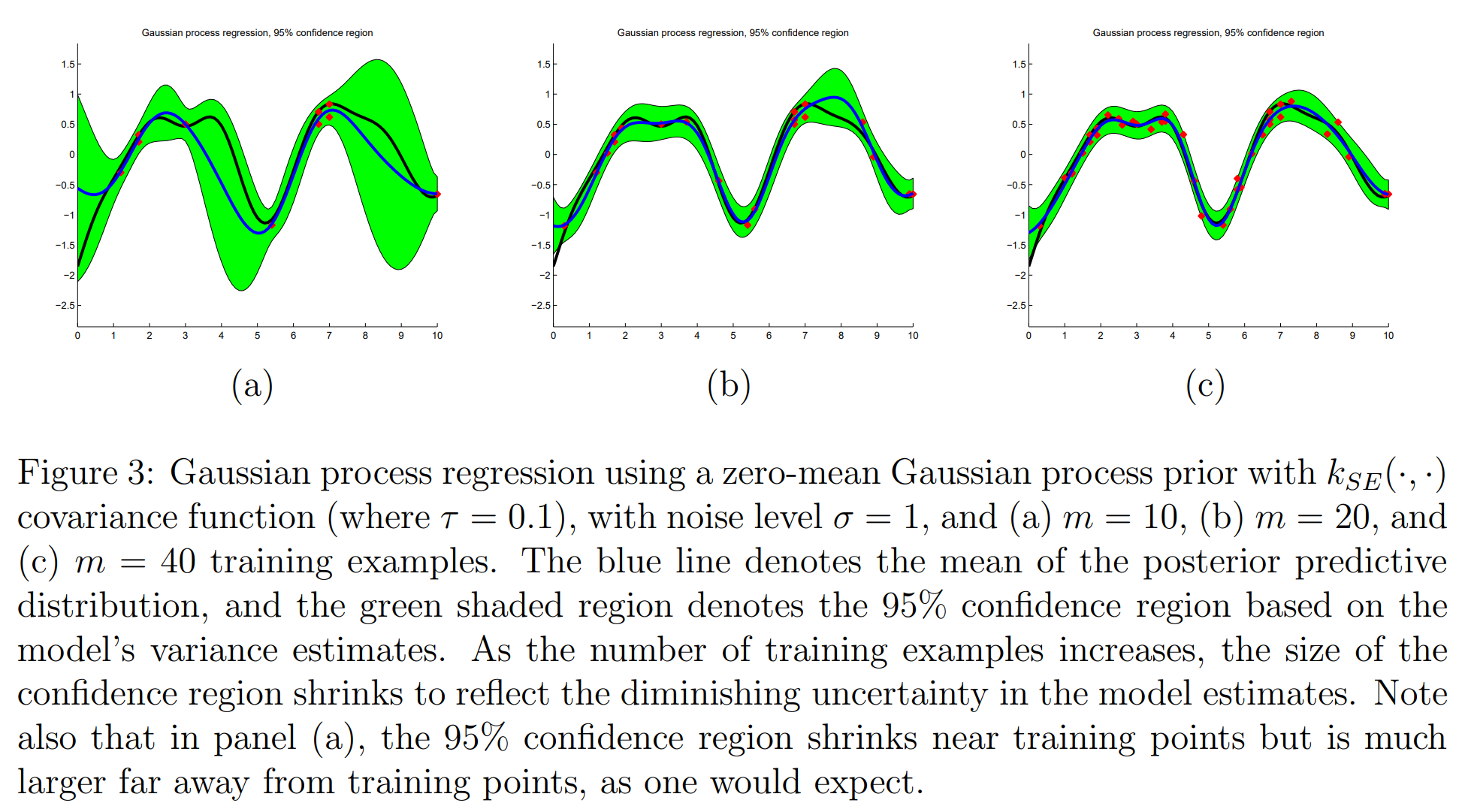
Gaussian Process Regression
“Machine Learning”을 공부하면서 개인적인 용도로 정리한 포스트입니다. 지적은 언제나 환영입니다 :)
본 글을 읽기 전에 “Distribution over functions & Gaussian Process“에 대한 글을 먼저 읽고 올 것을 권합니다 😉
기획 시리즈: Gaussian Process Regression
“Distribution over functions & Gaussian Process“를 통해 Gaussian Process로 함수에 대한 확률 분포(distribution over functions)를 어떻게 모델링하는지 살펴보았다. 이번 포스트에서는 distribution over functions가 Bayesian Regression의 패러다임 아래에서 어떻게 활용되는지를 살펴본다🙌
Gaussian Process Regression

먼저 <Gaussian Process Regression; 이하 GP Regression>을 수행하기 위한 셋업을 해보자.
i.i.d. sample의 모임인 train set $S = \{ (x_i, y_i)\}^m_{i=1} = (X, y)$은 unknown distribution에서 추출된 샘플이다. 이때, GP Regression은 아래와 같이 Regression model을 구축한다.
\[y_i = h(x_i) + \epsilon_i \quad (i = 1, \dots, m)\]이때 $\epsilon_i$는 i.i.d noise로 $\epsilon_i \sim N(0, \sigma^2)$이다.
<Bayesian Regression>에선 $y_i = \theta^T x_i + \epsilon_i$ 모델링한 것과 차이점이 있다.
이제 $h(\cdot)$에 대해 prior distribution over function에 대한 가정을 도입한다.1 ‘prior’가 붙은 것을 눈치챘다면 이것을 ‘posterior’로 갱신하리라는 것도 알아챌 것이다 🙌 먼저 $h(\cdot)$가 zero-mean GP라고 가정한다.
\[h(\cdot) \sim \mathcal{GP}(0, \; k(\cdot, \cdot))\]※ NOTE: $k(x, x’)$ is a valid covariance function.
이번에는 $S$와 동일한 unknown distribution에서 추출한 i.i.d. sample의 모임인 test set \(T = \left\{ x^{*}_i, y^{*}_i\right\}^{m_{*}}_{i=1} = (X^{*}, y^{*})\)를 살펴보자. 이전의 <Bayesian Regression>에서는 Bayes’ rule을 이용해 <parameter posterior> $p(\theta \mid S)$를 유도하고, 이것을 통해 <posterior predictive distribution> $p(y^{*} \mid x^{*}, S)$를 유도했다. 그런데 GP Regression에서는 훨씬 쉬운 방법으로 posterior predictive distribution을 유도할 수 있다!! 😲
Prediction
우리는 prior distribution over function $h(\cdot) \sim \mathcal{GP}(0, \; k(\cdot, \cdot))$을 정의했다. GP의 성질에 따라 $\mathcal{X}$의 subset인 $X, X^{*} \subset \mathcal{X}$에 대해 joint distribution $p(\vec{h}, \vec{h^{*}} \mid X, X^{*})$을 구하면 아래와 같다.
\[\begin{bmatrix} \vec{h} \\ \vec{h^{*}} \end{bmatrix} \mid X, X^{*} \sim \mathcal{N} \left( \vec{0}, \; \begin{bmatrix} K(X, X) & K(X, X^{*}) \\ K(X^{*}, X) & K(X^{*}, X^{*}) \end{bmatrix}\right)\]matrix-form의 표기가 많이 등장했지만 따로 표기를 설명하지는 않겠다 🙏
또 i.i.d. noise에 대해선 아래가 성립한다.
\[\begin{bmatrix} \vec{\epsilon} \\ \vec{\epsilon^{*}} \end{bmatrix} \sim \mathcal{N} \left( \vec{0}, \; \begin{bmatrix} \sigma^2 I & O \\ O & \sigma^2 I \end{bmatrix}\right)\]이제 이걸 종합하면,
\[\begin{bmatrix} \vec{y} \\ \vec{y^{*}} \end{bmatrix} \mid X, X^{*} = \begin{bmatrix} \vec{h} \\ \vec{h^{*}} \end{bmatrix} \mid X, X^{*} + \begin{bmatrix} \vec{\epsilon} \\ \vec{\epsilon^{*}} \end{bmatrix}\]가 되는데, independent Gaussian random variable의 합은 역시 Gaussian이므로
\[\begin{bmatrix} \vec{y} \\ \vec{y^{*}} \end{bmatrix} \mid X, X^{*} \sim \mathcal{N} \left(\vec{0} , \; \begin{bmatrix} K(X, X) + \sigma^2 I & K(X, X^{*}) \\ K(X^{*}, X) & K(X^{*}, X^{*}) + \sigma^2 I \end{bmatrix}\right)\]위의 식은 $p(\vec{y}, \vec{y^{*}} \mid X, X^{*})$에 대한 식으로 “joint distribution of the observed values and testing points”이다. regression은 testing points에 대한 분포를 원하므로 conditional distribution $p(\vec{y^{*}}, \mid \vec{y}, X, X^{*})$을 구하면 아래와 같다.
\[\vec{y^{*}}, \mid \vec{y}, X, X^{*} \sim \mathcal{N} \left( \mu^{*}, \; \Sigma^{*} \right)\]where ($K^{*} = K(X, X^{*})$)
\[\begin{aligned} \mu^{*} &= K^{*} \left( K + \sigma^2 I \right)^{-1}\vec{y} \\ \Sigma^{*} &= K^{**} + \sigma^2 I - {K^{*}}^T \left( K + \sigma^2 I \right)^{-1} K^{*} \end{aligned}\]유도 과정은 conditional distribution of multi-variate Gaussiaion distribution에 대한 식을 그대로 사용하면 된다. 🙌
Boom! 이것으로 우리는 posterior predictive distribution을 얻었다!! 🤩 이전의 Bayesian Linear Regression의 것과 비교해보면 GP Regression은 정말 계산적으로도 정말 간단한 형태임을 확인할 수 있다 👍
보충
앞에서 $h(\cdot)$가 ‘prior’ distribution over functions 라고 했다. 그럼 ‘posterior’ distribution over function을 유도하면, 위에서 언급한 joint distribution $p(\vec{h}, \vec{h^{*}} \mid X, X^{*})$에서 conditional distribution을 구하면 된다.
\[\begin{bmatrix} \vec{h} \\ \vec{h^{*}} \end{bmatrix} \mid X, X^{*} \sim \mathcal{N} \left( \vec{0}, \; \begin{bmatrix} K(X, X) & K(X, X^{*}) \\ K(X^{*}, X) & K(X^{*}, X^{*}) \end{bmatrix}\right)\]then, the conditional distribution is
\[\vec{h^{*}} \mid \vec{h}, X, X^{*} \sim \mathcal{N} \left( {K^{*}}^T K^{-1} \vec{h}, \; K^{**} - {K^{*}}^TK^{-1}K^{*}\right)\]가 된다. 이것이 posterior distribution over function $h(\cdot \mid X)$이다!
Insights
이번 문단에서는 GP Regression에 대한 통찰들에 대해 살펴볼 것이다. locally-weighted linear regression처럼 GP Regression은 non-parameteric regression model이다. 이는 input data의 함수에 선형에 대한 가정이나 다항식에 대한 가정을 할 필요가 없으며 arbitrary function을 다루는 것이 가능하다는 것을 말한다! 🤩 대학에서 들었던 “통계적 데이터마이닝(IMEN472)” 수업에서 non-parameteric model에 대해 다루긴 했는데, <GP Regression>은 다루지 않았다.
GP에서 사용했던 <squared exponential kernel> $k_{SE}(x, x’)$에 대해 살펴보자.
\[k_{SE}(x, x') = \exp \left( - \frac{1}{2\tau^2} (x - x')^2 \right) \quad (\tau > 0)\]hyper-parameter인 $\tau$는 smoothness를 조정하는 파라미터로 $\tau$ 값이 작을수록 가까이 있는 샘플을 주로 본다. 그래서 model의 fluctuation이 심해진다. 반대로 $\tau$ 값이 커지면, 멀리 있는 샘플도 반영하기 때문에 model이 smooth 해진다.
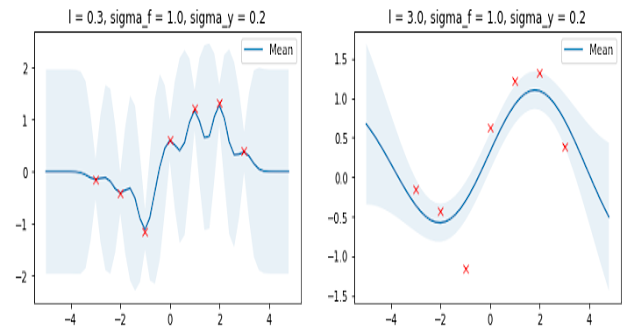
ref. ‘손쓰’님의 포스트
다음으로 regression noise인 $\sigma$(그림에서는 $\sigma_y$)가 있다. 이 녀석은 uncertainty의 정도를 결정하는 파라미터로 $\sigma$ 값이 클수록 데이터의 noise가 크다고 판단한다.
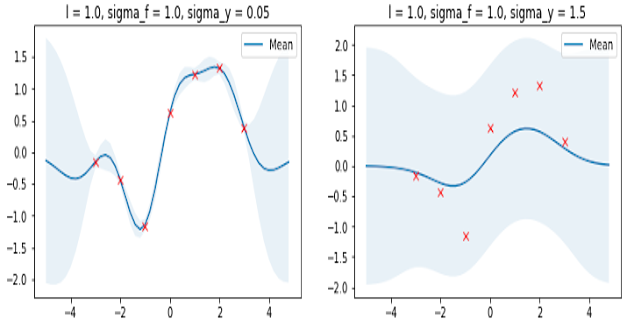
ref. ‘손쓰’님의 포스트
맺음말
지금까지 <GP Regression>에 대해 살펴보았다. 이 녀석은 bayesian regression model이면서 non-parameteric model인 녀석이었다. 게다가 <GP Regression>을 anomaly detection에 사용한다면, anomaly set에 대한 labeling 없이 unsupervised learning로 anomaly detection에 활용할 수 있다 😁 개인적으로 GP Regression은 실전에서도 굉장한 성능과 그럴듯한 결과를 도출했어서 꽤 만족했다 👍 위키피디아에서는 GP Regression을 “kriging”이라고 부르던데, 문서를 읽어보니 GP Regression에 대한 더 깊고 많은 내용을 다루고 있다. GP Regression이 더 궁금하다면 해당 문서를 읽어보자! 🙌
다음 시리즈로는 MCMC(Markov Chain Monte Carlo)를 생각하고 있다. 대학에서 ‘인공지능’ 과목 들을 때 보긴 했는데 그때는 제대로 이해를 못 했었다 😥
references
-
Bayesian Linear Regression에서도 prior distribution을 사용했는데, 그때는 parameter $\theta$에 대한 <parameter prior> 였다! 그러나 Bayesian Regression과 달리 GP Regression은 parameter $\theta$를 사용하지 않는 non-parameteric 모델이다!! 이에 대해선 뒷 문단에서 둘을 비교하며 한번 더 살펴보겠다 😉 ↩