Divide and Conquer
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Divide and Conquer
<분할 정복 Divide and Conquer>는 문제를 해결하는 접근법 중 하나다. 그 과정을 간략히 기술하면 아래와 같다.
- Break the problem into “subproblems”.
- Solve them recursively.
- Combine the solutions to get the answer to the problem.
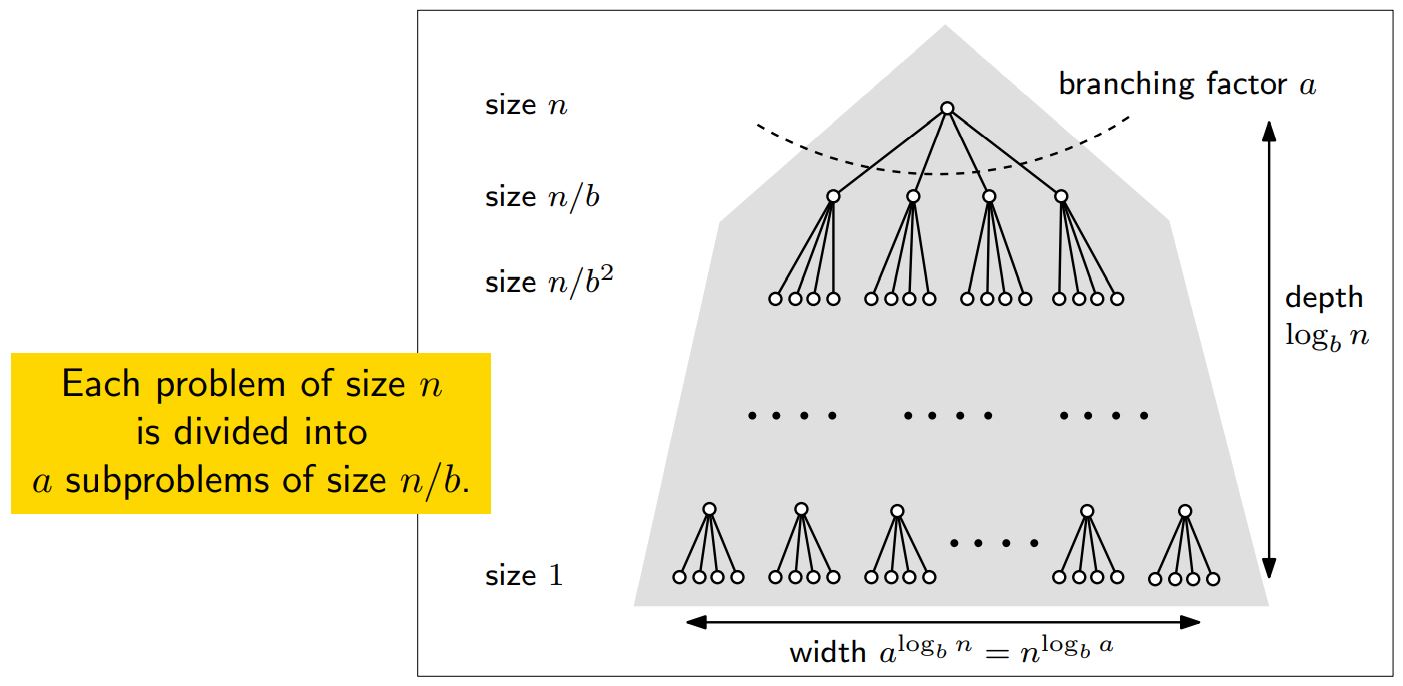
분할 정복은 기본적으로 <재귀 Recursion>을 기반으로 한다. 문제를 <하위 문제 subproblem>로 분할하고, 그 하위 문제를 더 하위의 문제로 분할한다. 분할은 손쉽게 다룰 수 있는 수준인 베이스 케이스 진행된다. 이후엔 분할한 규칙에 따라 하위 문제에서 얻은 결과를 상위 문제에서 차례대로 조합(Combine) 해주면 원래 문제에 대한 정답을 얻는다.
Master Theorem: Recurrence Relations
이 단락에서는 <분할 정복>의 시간 복잡도를 유도하는 좋은 도구인 <Master Theorem>에 대해 다룬다.
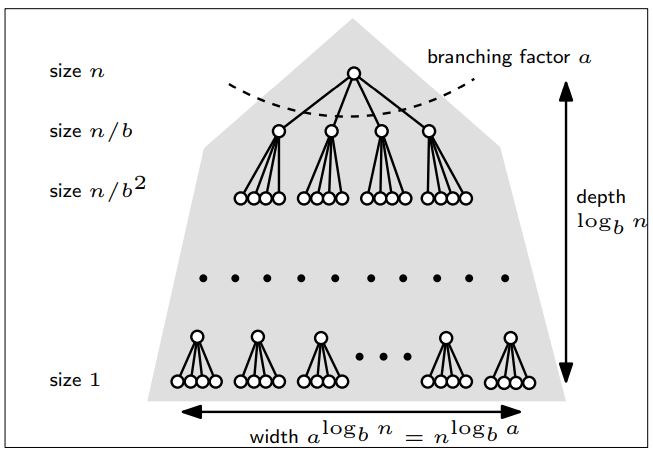
먼저 위와 같이 size $n$의 문제를 size $n/b$의 subproblem $a$개로 분할하는 경우를 고려해보자. 좀더 특정하자면, <branching fator>가 $a$, <분할의 깊이 depth>가 $\log_b {n}$인 상황이다. $O(n^c)$는 각 과정에서 드는 고정 비용이다.
이것을 재귀식으로 표현하면 아래와 같다.
\[T(n) = a \cdot T(\lceil n/b \rceil) + O(n^c)\]<Master Theorem>은 분할 정복의 계산 복잡도가 $a$와 $b$, $c$의 관계에 따라 아래와 같이 유도됨을 기술한다.
\[T(n) = \begin{cases} O(n^c) &\mbox{if } c > \log_b {a} \\ O(n^d \log {n}) & \mbox{if } c = \log_b {a} \\ O(n^{\log_b {a}}) & \mbox{if } c < \log_b {a} \end{cases}\]$a$, $b$, $c$에 대한 값만 안다면, 계산 복잡도를 바로 얻을 수 있다니! 얼마나 편리한 정리인가!! 한번 증명해보자! 🤩
proof.
At $k$-th level, we get $a_k$ subproblems of size $n/b^k$. Also we should consider fixed cost $O(n^c)$ too. At $k$-th level, the size of problem is $n/b^k$, so fixed cost is $O\left(\left(n/b^k\right)^c\right)$.
Then, the cost at $k$-th level is
\[a^k \cdot O\left(\left(n/b^k\right)^c\right)\]We will slightly modify the given form of cost as below.
\[a^k \cdot O\left(\left(n/b^k\right)^c\right) = O(n^c) \cdot \left( a/b^c \right)^k\]There are $\log_b {n}$ levels of division process, so let’s sum up the cost at each level.
\[\sum^{\log_b {n}}_{k=0} O(n^c) \cdot \left( a/b^c \right)^k\]Then, given series is a geometric series with ratio $a/b^c$.
The simple way to understand geometric series is watching the ratio!
Case 1. if ratio $a/b^c < 1$, then the series decreases.
Case 2. if ratio $a/b^c = 1$, then the series is a just constant sum up.
Case 3. if ratio $a/b^c > 1$, then the series increases.
- In Case 1, take the 1st term, $\implies$ $O(n^c)$
- In Case 2, take sum, $\implies$ $O(n^c) \cdot \log_b {n} = O(n^c \log_b {n}) = O(n^c \log n)$
- In Case 3, take the last term, $\implies$ $O(n^c) \cdot \left(a/b^c\right)^{\log_b {n}} = O(n^c) \cdot \frac{a^{\log_b n}}{n^c} = O\left( n^{\log_b a} \right)$
Therefore,
\[T(n) = \begin{cases} O(n^c) &\mbox{if } c > \log_b {a} \\ O(n^d \log {n}) & \mbox{if } c = \log_b {a} \\ O(n^{\log_b {a}}) & \mbox{if } c < \log_b {a} \end{cases}\]$\blacksquare$
아래는 <분할 정복>을 이용해 해결하는 대표적인 주제들에 대해 정리한 포스트들이다.
