Introduction to Hypothesis Tests
“확률과 통계(MATH230)” 수업에서 배운 것과 공부한 것을 정리한 포스트입니다. 전체 포스트는 Probability and Statistics에서 확인하실 수 있습니다 🎲
Statistical Hypothesis
Definition. Statistical Hypothesis
A <statistical hypothesis> is a statement about the population distribution, usually, in terms of the parameter values.
Example.
Supp. we have a p-coin, I believe that it is a fair coin, on the other hand, you think it is a biased coin, in particular, you believe that $p=0.7$. What can we do?
- $H_0: p = 0.5$
- $H_1: p = 0.7$
Definition. Null Hypothetsis $H_0$ & Alternative Hypothesis $H_1$
- Null Hypothetsis $H_0$: a hypothesis we expect to reject
- Alternative Hypothesis $H_1$: a hypothesis we set out to prove
Q. How do we do <Hypothesis Test>?
A. First, we should set a <Test Statistic>!
Let’s toss a coin $n$-times independently. For each toss, let $X_i$ are $1$ for head and $0$ for otherwise.
Then, $X := \sum X_i$, the (# of heads in $n$ tosses) be $X \sim \text{BIN}(n, p)$.
Then, we can use $X$ as a <Test Statistic>!
우리는 이 <Test Statistic>로 가설 $H_0$를 reject 하거나 reject 하지 않을 것이다!
위의 $H_0: p=0.5$, $H_1: p=0.7$의 경우에서 생각해보자. 만약 $X$가 large enough, 즉 “$X \ge C$ for some $C$”라면, $H_0$를 reject 하는게 합리적이다.
우리는 이 $H_0$를 reject하는 기준이 되는 범위 $X \ge C$를 <rejection region> 또는 <critical region>이라고 하며, 이 범위를 잡을 때 쓰는 값 $C$를 <critical value>라고 한다!
T1 Error & T2 Error
Q. How to choose $C$?
<critical value> $C$의 값을 잡기 위해서는 <Type 1 Error>, <Type 2 Error>를 살펴봐야 한다.
| reject $H_0$ | not reject $H_0$ | |
|---|---|---|
| $H_0$ is true | Type 1 Error | good |
| $H_0$ is false | good | Type 2 Error |

이 사진이 Type 1, Type 2 Error를 가장 잘 표현하는 사진인 것 같다 ㅋㅋㅋ
Case. Type 1 error; $\alpha$ error; 잘못된 인정
이때, $P(T1)$을 최대한 줄이려면, $C$를 최대한 키워서 웬만한 경우가 아니면 $X$가 $X \ge C$의 조건을 만족시키지 못 하도록 만들면 된다. 즉, $H_0$를 reject 하는 기준을 빡세게 만든다.
Case. Type 2 error; $\beta$ error; 잘못된 부정
이때, $P(T2)$를 최대한 줄이려면, $C$를 최대한 줄여서 웬만하면 $X$가 $X \ge C$를 만족 시키도록 만들면 된다. 즉, 웬만하면 $H_0$를 reject하게 만든다.
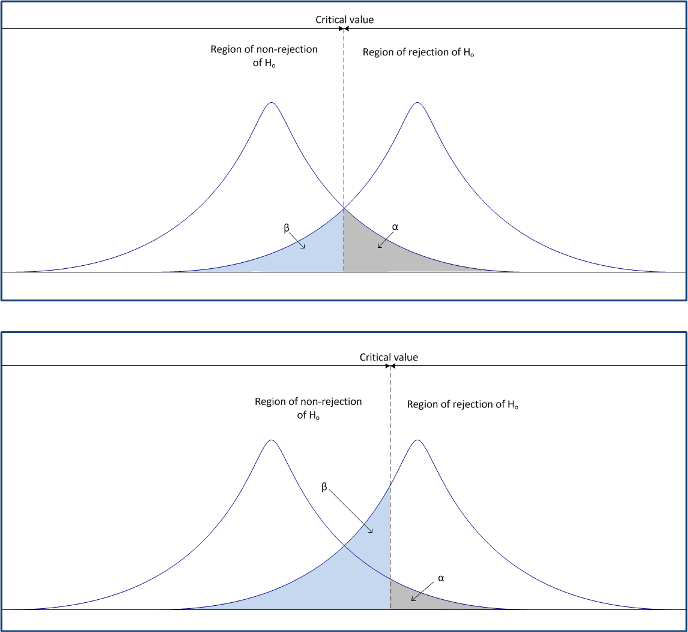
?? 뭔가 이상하다. $P(T1)$를 줄이려면, $C$를 키워야 하고, $P(T2)$를 줄이려면, $C$를 줄여야 한다. 😕 뭐가 맞는 걸까?
답은 $P(T1)$과 $P(T2)$, 둘 중 하나만 가능한 작게 만들 수 있다는 것이다 😱
그럼 또다른 질문이 떠오른다.
Q. $P(T1)$과 $P(T2)$ 중 어느 것을 줄여야 좋을까?
아래의 경우를 생각해보자.
- $H_0$: 피고 A is innocent
- $H_1$: 피고 A is guilty
이때, T1 & T2 error가 무엇을 의미하는지 잘 보자.
- T1 error: $H_0$가 사실인데, $H_0$를 reject
- T2 error: $H_1$이 사실인데, $H_1$을 reject
두 상황 중 뭐가 더 안 좋을까? 당연히 “T1 error”의 경우다! 왜냐하면, 무고한 사람을 유죄라고 선고했기 때문이다!
“암 진단”이라는 다른 상황을 생각해본다면,
- $H_0$: 환자 B는 건강하다.
-
$H_1$: 환자 B는 암이 있다.
- T1 error: 사실 환자 B가 건강한데, 암 환자로 진단
- T2 error: 사실 환자 B가 암이 있는데, 건강하다고 진단
이 경우에서도 건강한 사람을 암 환자로 진단해 엄청난 돈을 쓰게 했으니 “T1 error”가 더 안 좋다.
위와 같은 상황을 바탕으로, 둘 중 하나만 줄일 수 있다면, “T1 error”를 최대한 줄여라는 결론을 얻는다.
그럼 “T2 error”는?? “T2 error”는 운에 맡긴다고 한다 ㅋㅋㅋ
그 이유는 T2 error의 경우, “not reject $H_0$”라는 결과가 나오는데, 이것이 “$H_1$를 accept한다”와는 다른 의미이기 때문이다. 결국 T2 error에서는 $H_0$에 대해서도 $H_1$에 대해서도 어떤 진술도 할 수 없기 때문에, 그나마 괜찮다고 보는 것이다!
Significance Level; $\alpha$
Definition. Significance level; size of a test; 유의 수준 $\alpha$
The probability of committing a <Type 1 Error> is called the <significance level>, and we use $\alpha$ to denote the significance level.
\[\alpha = P(\text{T1 Err}) = P(\text{reject} \; H_0 \mid H_0 \; \text{is true})\]💥 commonly used values for $\alpha$ are $0.1$, $0.05$, $0.01$.
💥 Interval Estimation을 수행할 때, 비슷한 것을 봤었다! 바로 <Confidence Level> $1-\alpha$다!
$\alpha$는 1종 오류의 가능성이다. Critical Value $C$에 의존하는 값으로 $C$가 엄격해질 수록 1종 오류의 가능성인 $\alpha(C)$의 값은 줄어들 것이다.
보통은 1종 오류의 상한선은 $0.1$, $0.05$, $0.01$ 정도로 설정하고, 이것을 <p-value>와 비교한다. <p-value>는 아래에서 곧 다룰 것이다.
Example.
$H_0: p=0.5$ vs. $H_1: p=0.7$
We toss a coin 20 times independently and obtained 14 heads. Test this at $\alpha = 0.0577$.
Solve.
Let $X = \sum X_i \sim \text{BIN}(20, p)$.
The critical region is $\{ X \ge C \}$.
Here, $\alpha = P(X \ge C \mid p=0.5) = P(\text{BIN}(20, 0.5) \ge C)$.
Then, by the cdf of $\text{BIN}(20, 0.5)$,
\[P(\text{BIN}(20, 0.5) \le 13) = 0.9423\]Therefore, $C = 14$.
We will reject $H_0$ if (# of heads in 20 tosses) is $\ge 14$.
Since $x=14$, we reject $H_0$ at $\alpha = 0.0577$. $\blacksquare$
Now, we consider T2 error case! If T2 error is small, then we might accept $H_0$.
Example.
(Same situation with the above example)
Solve.
We’ve found that $C=14$ from the privous example. Then,
\[P(\text{BIN}(20, 0.7) \le 14) = 0.392 \approx 0.4\]If we fail to reject $H_0$, then we can’t accept $H_0$ because $P(T2)$ is too height to not accept $H_0$.
Example.
(Now, everything is same but $H_1: p=0.8$)
Solve.
The critical point $C$ is same as the previous one, because $H_0$ doesn’t change. → $C=14$
Now, T2 Error is
\[P(\text{T2 Err}) = P(X < 14 \mid p=0.8) = P(\text{BIN}(20, 0.8) < 14>) \approx 0.0867\]In this time, if we fail to reject $H_0$, then we can accept $H_0$!!
Power of Test; $\gamma(\theta)$
Definition. Power of Test; 검정력
The <power of a test> $\gamma(\theta)$ at $\theta=\theta_1$ is defined as the probability of rejection of $H_0$ when $\theta=\theta_1$ is a true value.
\[\gamma(\theta_1) = P(\text{reject} \; H_0 \mid \theta = \theta_1)\]💥 NOTE: $1-P(\text{T2 Err}) = \gamma(\theta_1)$
즉, <power of test>는 Null hypo $H_0$가 거짓일 때, $H_0$를 기각시키는 확률이다!
<검정력>은 T2 Error가 클수록 그 값이 작아진다! 그래서 <검정력>을 높이고 싶다면, T2 Error를 줄이는 적절한 Alternative Hypothesis $H_1: \theta = \theta_1$를 제시해야 한다.
이 <power of test>는 아래 상황일 때, 그 값이 커진다.
- T2 Error를 줄이는 적절한 Alternative Hypothesis $H_1: \theta = \theta_1$
- <significance level> $\alpha$ ▲
- 표본의 크기 $n$ ▲
p-value
지금까지 우리는 <significance level> $\alpha$ 값을 $0.1$, $0.05$ 등으로 설정하고, 이에 따른 <critical value> $C$를 구하고, 이걸 Test Statistics $X$와 비교해서 $H_0$를 기각할지 결정했다. 그런데 $\alpha$ 값을 설정하지 않고, Critical Value $C$를 reject이 가능한 경계인 $C = X$로 설정한 후, $\alpha$을 역으로 구할 수 있지 않을까? <p-value>가 딱 그런 녀석이다!
Definition. p-value; 유의 확률
The <p-value> of a test is the lowest significance level at which $H_0$ can be rejected with the given data.
주어진 데이터의 Test Statistic $X$를 기준으로 $H_0$를 reject 할 수 있는 가장 작은 $\alpha$ 값이 바로 <p-value>이다!
Q. 왜 ‘가장 작은’ $\alpha$ 값일까?
A. T1 Error에 대해 얘기할 때, Critical Value $C$를 빡세게 잡을 수록 T1 Error의 가능성이 줄어든다고 했다. 즉, $C$가 빡셀 수록 $\alpha$ 값이 작아진다. 보통은 $X > C$이기에 $H_0$를 reject 하는데, 이걸 경계인 $C = X$까지 $C$ 값을 끌어올림으로써 $\alpha$ 값을 최대한 낮춘 것이다. 이런 이유 때문에 <p-value>가 작을 수록 정해둔 $C_{0.1}$, $C_{0.05}$ 값보다 더 빡센 조건에서도 $H_0$가 reject 됨을 말한다.
예를 통해 제대로 이해해보자!
Example.
Everything is same to above situation.
- $H_0: p = 0.5$
- $H_1: p = 0.7$
Toss a coin 20 times independently, and obtained 14 heads.
BUT, in this time, we don’t have significance level $\alpha$!!
Solve.
The rejection region is $\{ X \ge C\}$.
$X = 14$라는 주어진 데이터에서 $H_0$를 기각하려면, $X=14$가 저 rejection region에 포함되어야 한다. $X$가 rejection region에 포함되도록 하는 가장 작은 $C$ 값은 $C=14$이다!
어랏? 우리는 이미 $C=14$일 때의 T1 Error를 구했다.
\[0.0577 = P(\text{BIN(20, 0.5)} \ge 14)\]즉, significance level $\alpha=0.0577$가 $H_0$를 기각하는 가장 작은 값이다. $0.0577$이 이번 검정(Test)의 “p-value”다!!
우리는 “p-value”를 지표로 삼아 $H_0$를 기각할지 결정할 수 있다.
만약, significance level $\alpha$와 비교했을 때, “p-value”의 값이 더 작다면, 즉 $\alpha$가 생성하는 넓이가 “p-value”가 생성하는 넓이를 포함한다면, 이것은 주어진 데이터가 $\alpha$의 critical region에 속한다는 말이기 때문에, $H_0$를 기각한다!
반대로 “p-value”의 값이 크다면, $H_0$를 기각할 수 없다.
보통 p-value가 5%(=0.05)보다 작다면 “유의한 차이가 있다”고 얘기한다. 이때 ‘유의한 차이’는 실험으로 얻은 결과가 기존 이론인 $H_0$이 예상하는 결과와 차이가 크다는 것을 말한다. 따라서 기존 이론 $H_0$를 reject 해야 한다는 결론을 유도한다.
개인적으로 <p-value>는 그 의미가 자주 헷갈려서 여러 의미와 해석을 함께 보면 도움이 될 것 같다.
- $H_0$를 reject 할 수 있는 가장 작은 $\alpha$ 값
- 기존 이론 $H_0$가 맞다는 가정 하에, 얻어진 Test Statistic $X$가 나올 확률.
- 이 확률이 낮다는 것은 기존 이론 $H_0$가 맞다는 가정이 틀린 것이 된다. (통게적 귀류법)
- 실험 결과가 기존 이론 $H_0$와 양립하는 정도를 $[0, 1]$의 수치로 표현한 것.
- <p-value> 값이 작을수록 데이터와 기존 이론 $H_0$는 양립 불가능
- 우연성의 정도
- <p-value>가 낮을 수록, 실험 결과가 우연이 아닐 거라는 말
맺음말
이제 “통계적 검정(Statistical Test)”를 수행하기 위해 필요한 기본적인 내용은 다 살펴봤다. 다음 포스트부터 상황에 따라 통계적 검정을 어떻게 수행하는지 살펴볼 예정이다. 그렇게 어렵진 않고, 요구하는 것들을 잘 파악해서 순서에 맞게 계산하기만 하면 된다.
우리가 추정(Estimation)에서 살펴본 순서와 동일하게 검정(Testing)을 살펴보자.
