NP-hard and NP-complete
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
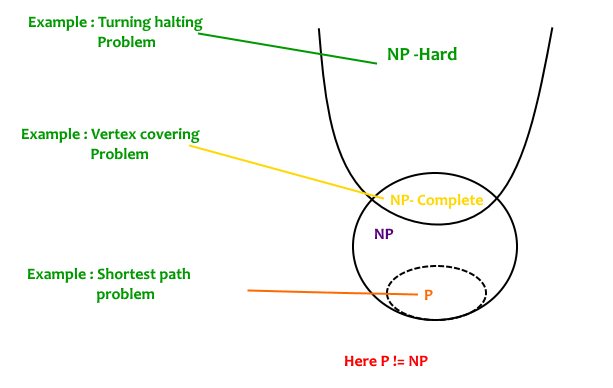
“P and NP” 포스트에서 $\textbf{NP}$ 문제는 non-deterministic and polynomial-time solvable한 문제를 말했다. 또는 set of all search problems라고도 했다. 그런데 위의 그림을 보면, $\textbf{P}$와 $\textbf{NP}$ 외에도 “$\textbf{NP-complete}$”, “$\textbf{NP-hard}$”라는 클래스가 눈에 보인다. 이번 포스트에서는 그들에 대해 살펴보겠다.
NP-hard
Complexity Space를 표현한 위의 그림을 보면, $\textbf{NP-complete}$가 $\textbf{NP}$와 $\textbf{NP-hard}$의 교집합인 것을 볼 수 있다. 그래서 $\textbf{NP-complete}$를 이해하기 위해선 $\textbf{NP-hard}$를 이해해야 한다.
Definition. $\textbf{NP-hard}$
A problem $x$ is $\textbf{NP-hard}$ if every problem $y \in \textbf{NP}$ reduces to $x$.
즉, $\textbf{NP}$에 속하는 모든 문제를 polynomial-time reduction 할 수 있는 문제라면, 그 문제가 $\textbf{NP-hard}$라는 말이다. Reduction의 의미를 생각했을 때, $A \le_p B$가 “문제 $B$가 문제 $A$보다 더 어렵다”는 사실을 말해주니, 모든 문제가 환원되는 대상이라면 그 문제는 정말정말정말로 어려운 문제일 것이다. 그래서 “hard”라는 표현이 붙었다.
$\textbf{NP-hard}$ is ‘harder’ than any problem of $\textbf{NP}$, in other words, ‘harder’ than any search problem.
$\textbf{NP-hard}$에 속하는 대표적인 문제로는 <Halting Problem>이 있다. CS에서 워낙 유명한 Undecidable 문제이기에 해당 문제에 대해 잘 설명한 영상으로 설명을 대체한다.
<Halting Problem>의 경우 Search Problem이 아니기에 $\textbf{NP}$에 속하지 않는다. 그러나 $\textbf{NP}$에 속하는, 즉 search problem인 $\textbf{NP-hard}$ 문제도 존재한다. 그것이 바로 아래에서 살펴볼 $\textbf{NP-complete}$ 문제다!
NP-complete
Definition. $\textbf{NP-complete}$
A problem $x$ is $\textbf{NP-hard}$ if $x \in \textbf{NP}$ and $x \in \textbf{NP-hard}$.
$\textbf{NP}$와 $\textbf{NP-hard}$의 교집합라는 의미를 그대로 담은 $\textbf{NP-complete}$의 정의다. Search Problem에 속하는 $\textbf{NP-hard}$라는 의미인데, 대표적인 문제로 SAT 문제가 $\textbf{NP-complete}$ 문제다.
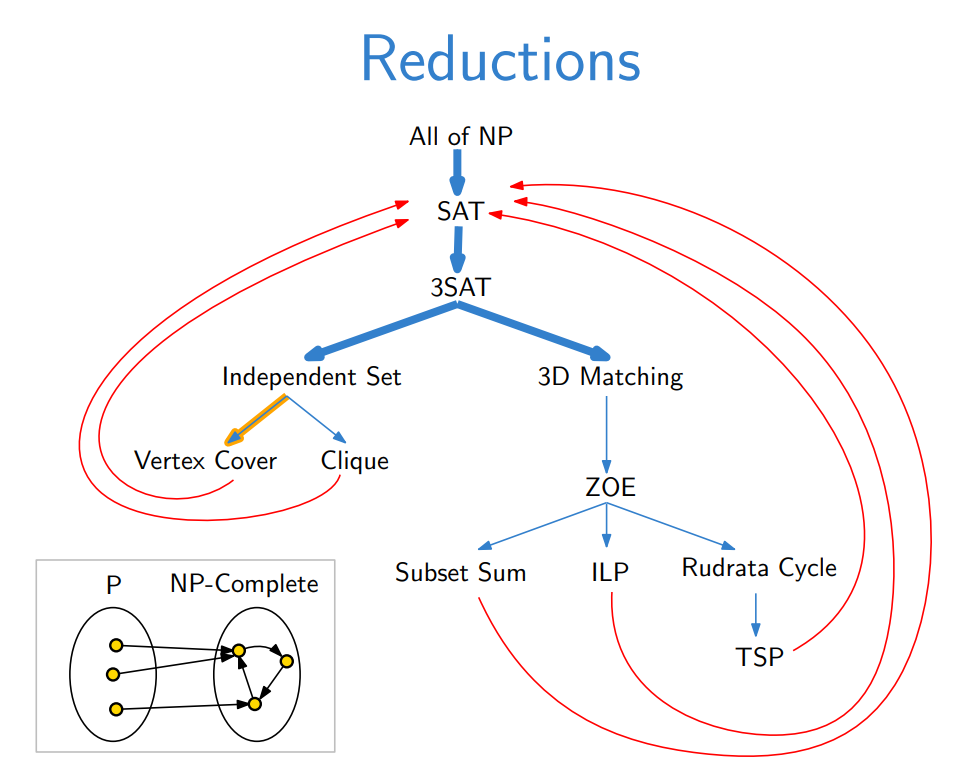
이전 포스트에서는 $\textbf{NP-complete}$를 아래와 같이 정의했는데, 이것도 맞는 표현이다.
Definition. $\textbf{NP-complete}$
A search problem is $\textbf{NP-complete}$ if all other search problems reduce to it.
모든 Search Problem, 즉 $\textbf{NP}$ Problem이 해당 문제로 Reduction 가능하다면, 해당 문제는 $\textbf{NP-complete}$라는 말이다. 놀랍게도 <Reduction>을 통해 $\textbf{NP-complete}$에 속하는 문제가 SAT 문제 하나가 아니고, 3-SAT, Independent-Set, 3D-Matching 문제 등이 SAT 문제로부터 환원되며, 또 SAT로 문제로 환원됨이 증명되었다. 그래서 지금까지 몇 개의 포스트에 걸쳐 살펴보았던 $\textbf{NP}$ 문제들은 모두 $\textbf{NP-complete}$이다!
결국 $\textbf{NP-complete}$를 온전히 이해하기 위해서 각종 $\textbf{NP}$ 문제부터, $\textbf{NP-hard}$의 개념까지 숙지해야 했다. 다음 포스트부터 각종 $\textbf{NP}$ 문제들이 어떻게 Reduction 되는지를 하나하나 살펴보자.
- Reduction (2)
- Reduction (3)
- Reduction (4)
