Reduction (4): Circuit-SAT and Cook-Levin Theorem
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Circuit-SAT is NP-complete
Circuit-SAT
먼저 Circuit-SAT가 무엇인지부터 살펴보자.
Definition. Circuit-SAT
Given a combinatorial circuit build out of $\text{AND}$, $\text{OR}$ and $\text{NOT}$ gates, is there a way to set the circuit inputs so that the output is $1$?
Circuit-SAT는 그저 boolean formula가 $\text{true}$인지 $\text{false}$인지를 판단하는 문제다. SAT 문제가 CNF 꼴의 boolean formula가 $\text{true}$인지 $\text{false}$인지를 판단하는 문제이기 때문에 Circuit-SAT는 SAT 문제를 generalization한 것인 셈이다. 실제로 SAT 문제를 Circuit-SAT 문제로 표현하는 것은 $\text{AND}$, $\text{OR}$, $\text{NOT}$ 게이트를 적절히 사용해 표현할 수 있음을 쉽게 이해할 수 있다.
\[\text{SAT} \le_P \text{Circuit-SAT}\]Overview
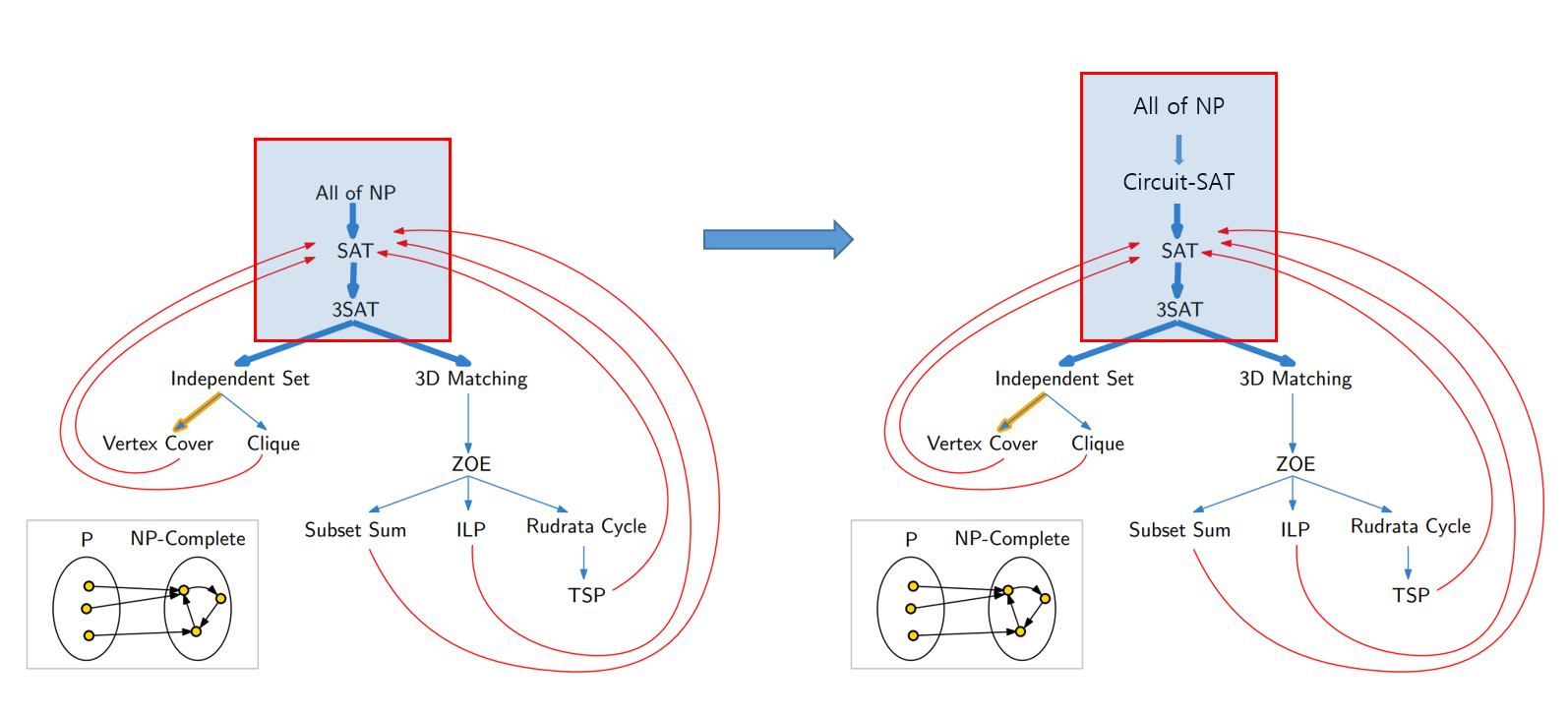
이번 포스트에서 우리의 목적은 모든 $\textbf{NP}$ 문제가 SAT 문제로 환원되는 것을 보이는 것이다. 이것은 SAT가 $\textbf{NP-complete}$임을 증명하는 것이다. 이를 증명하기 위해선 하나의 중간 단계를 추가하는데 그것이 바로 <Circuit-SAT>이다! 우리는 모든 $\textbf{NP}$ 문제가 Circuit-SAT 문제로 환원됨을 보이고, Circuit-SAT 문제를 SAT로 환원하는 방식을 살펴볼 것이다. 그리고 최종적으로 SAT 문제가 3-SAT 문제로 환원됨을 보일 것이다. 이것은 우리가 Reduction (2), Reduction (3) 포스트에서 살펴본 <Independent Set>, <Vertex Cover> 등의 문제가 $\textbf{NP-complete}$에 속함을 말한다.
증명은 위-아래 순서대로 하지 않고, 본인이 이해하기 편했던 순서대로 진행하겠다.
- SAT → 3-SAT
- Circuit-SAT → 3-SAT
- All of NP → Circuit-SAT: Cook-Levin Theorem
SAT → 3-SAT
제일 먼저 <SAT>가 <3-SAT>로 환원됨으로 보이자. 이 경우는 좀 특이한 상황인데, <SAT>는 <3-SAT>는 generalization인 반면에 <3-SAT>는 <SAT>의 special case이기 때문이다. 그래서
\[\text{3-SAT} \le_P \text{SAT}\]는 generalization과 special case에 의해 자연스럽게 유도되는데, 우리가 증명할 것은
\[\text{SAT} \le_P \text{3-SAT}\]이기 때문이다. 그러나 놀랍게도 이 Reduction이 가능하다!
Proof
[Problem Transformation]
3개 이상의 literal을 가진 clause $(a_1 \lor a_2 \lor \cdots \lor a_k) \, (k > 3)$를 아래의 방식으로 3-SAT으로 변환한다.
\[(a_1 \lor a_2 \lor \cdots \lor a_k) = (a_1 \lor a_2 \lor y_1)(\bar{y}_1 \lor a_3 \lor y_2)(\bar{y}_2 \lor a_4 \lor y_3) \cdots (\bar{y}_{k-3} \lor a_{k-1} \lor a_k)\]이때, $y_i$는 모두 새로운 boolean variable이다. 그런데 이런 변환이 말이 되는 걸까? Why this work?
[Solution Transformation]
clause $(a_1 \lor a_2 \lor \cdots \lor a_k) = \text{true}$가 되려면, 적어도 하나의 $a_i$는 $\text{true}$여야 한다.
-
그러나 만약 $a_i$ 모두 $\text{false}$라면, 모든 $y_i$는 $\text{true}$가 되더라도, 마지막 clause \((\bar{y}_{k-3} \lor a_{k-1} \lor a_k)\)가 $\text{false}$가 되어서 3-SAT으로 변환한 clause가 not satisfying 하다.
-
만약 어떤 $a_i=\text{true}$라고 하자. 그러면, $y_1, y_2, \dots, y_{i-2}$까지 모두 $\text{true}$이고, $y_{i-1}$부터 모두 $\text{false}$가 되면, 3-SAT으로 변환한 clause가 satisfying 한다.
즉, 3-SAT transformed SAT가 satisfiable하면, 위의 특성을 활용해 원본 SAT의 satisfiability와 truth assignment를 알 수 있다는 것이다!
Circuit-SAT → 3-SAT
우리는 이미 <Circuit-SAT>가 <SAT>의 generalization임을 안다.
\[\text{SAT} \le_P \text{Circuit-SAT}\]그러나 이번에 증명하는 건, 반대 방향인
\[\text{Circuit-SAT} \le_P \text{SAT}\]이다. 바로 위에서 살펴본 “SAT → 3-SAT”처럼 special case를 generalization으로 환원하는 것이다!
Proof
[Problem Transformation]
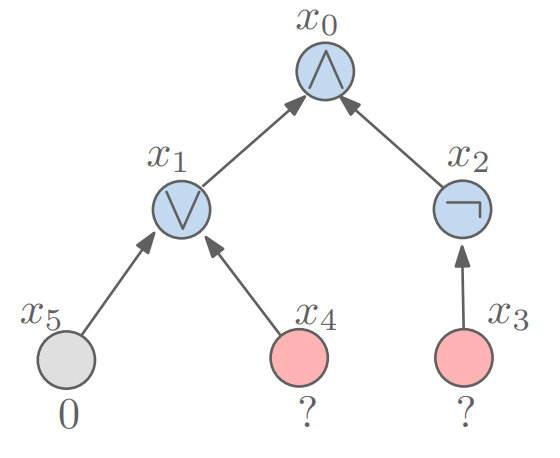
Circuit Instance $k$에 대해 각 노드를 모두 3-SAT variable $x_i$로 변환한다. 규칙은 아래와 같다.
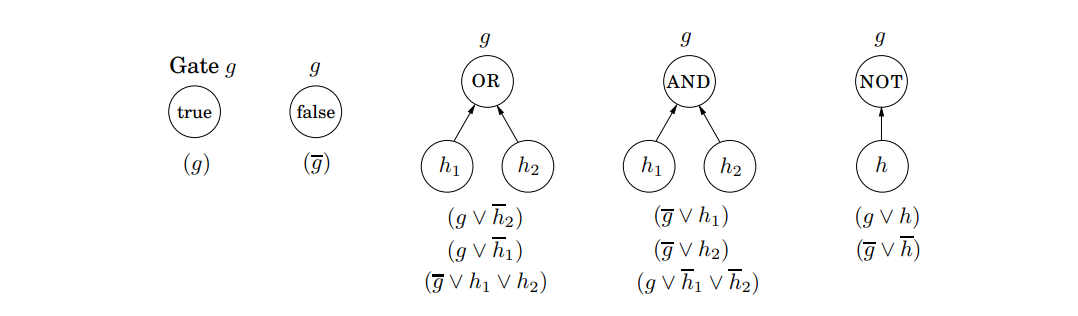
All of NP → Circuit-SAT: Cook-Levin Theorem
‘모든’ NP 문제라니! 지금까지 다룬 환원 중에서 가장 추상적인 형태의 환원이다. 흐름을 잘 따라가는게 중요한데, 일단 본격적인 증명을 하기 전에 아래의 논증을 먼저 이해하자.
어떤 문제 $X$가 $\textbf{NP}$에 속한다는 건, 문제 $X$가 Search Problem이라는 말이다. Problem $X$가 Search Problem이므로 polynomial-time algorithm인 verifier가 존재한다, 그것을 verifier $V$라고 하자. verifier $V$는 2가지를 입력으로 받는데, Problem $X$의 instance $x \in X$, 그리고 어떤 solution $s$이다: $V(x, s)$.
이때, 고정된 크기의 $n$ bits를 입력으로 받은 $\text{yes}/\text{no}$를 출력하는 어떤 알고리즘도 회로(circuit)으로 표현할 수 있다. 또, 이 회로 변환 과정은 입력 비트 $n$에 대해 polynomial-time 만에 가능하고, 그 회로의 크기도 입력 비트 $n$에 대해 polynomial-size이다. (본인은 대충 computer로 구현할 수 있으니 회로(circuit)으로 표현할 수 있다고 이해했다.)
위의 알고리즘을 회로 변환로 변환할 수 있다는 사실을 바탕으로 verifier $V(x, s)$를 circuit $C(x, s)$로 변환할 수 있다.
자, 이제 준비 과정은 끝났고, 본격적으로 Problem $X$를 <Circuit-SAT>로 환원해보자!
Proof
[Problem Transformation]
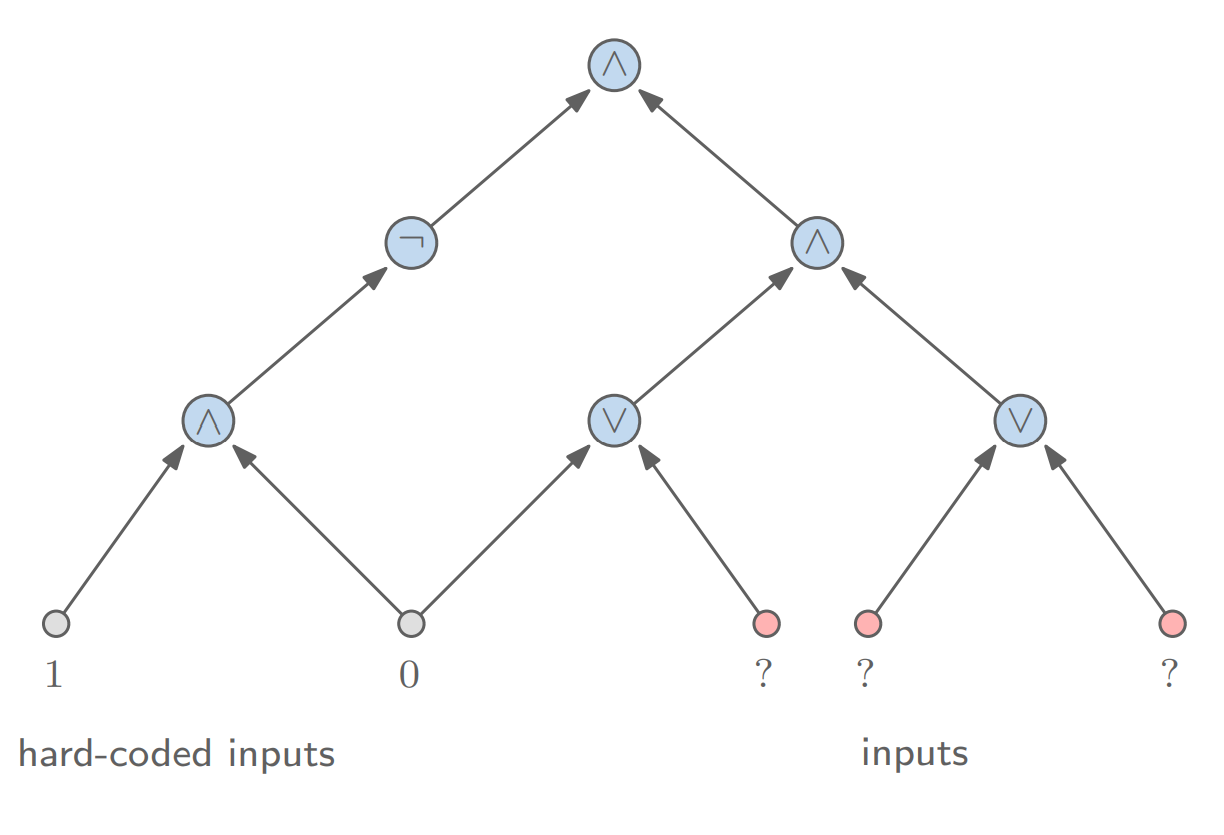
앞선 논의를 통해 Search Problem $X$의 Vertifier $V(x, s)$를 circuit $C(x, s)$로 변환할 수 있었다. 자, 이제 그 circuit $C(x, s)$가 어떻게 생겼는지 살펴보자.
첫째, problem instance인 $x$를 hard-coded input이다. 둘째, problem solution $s$는 Circuit-SAT 문제가 찾아야 하는 truth assignment이다!
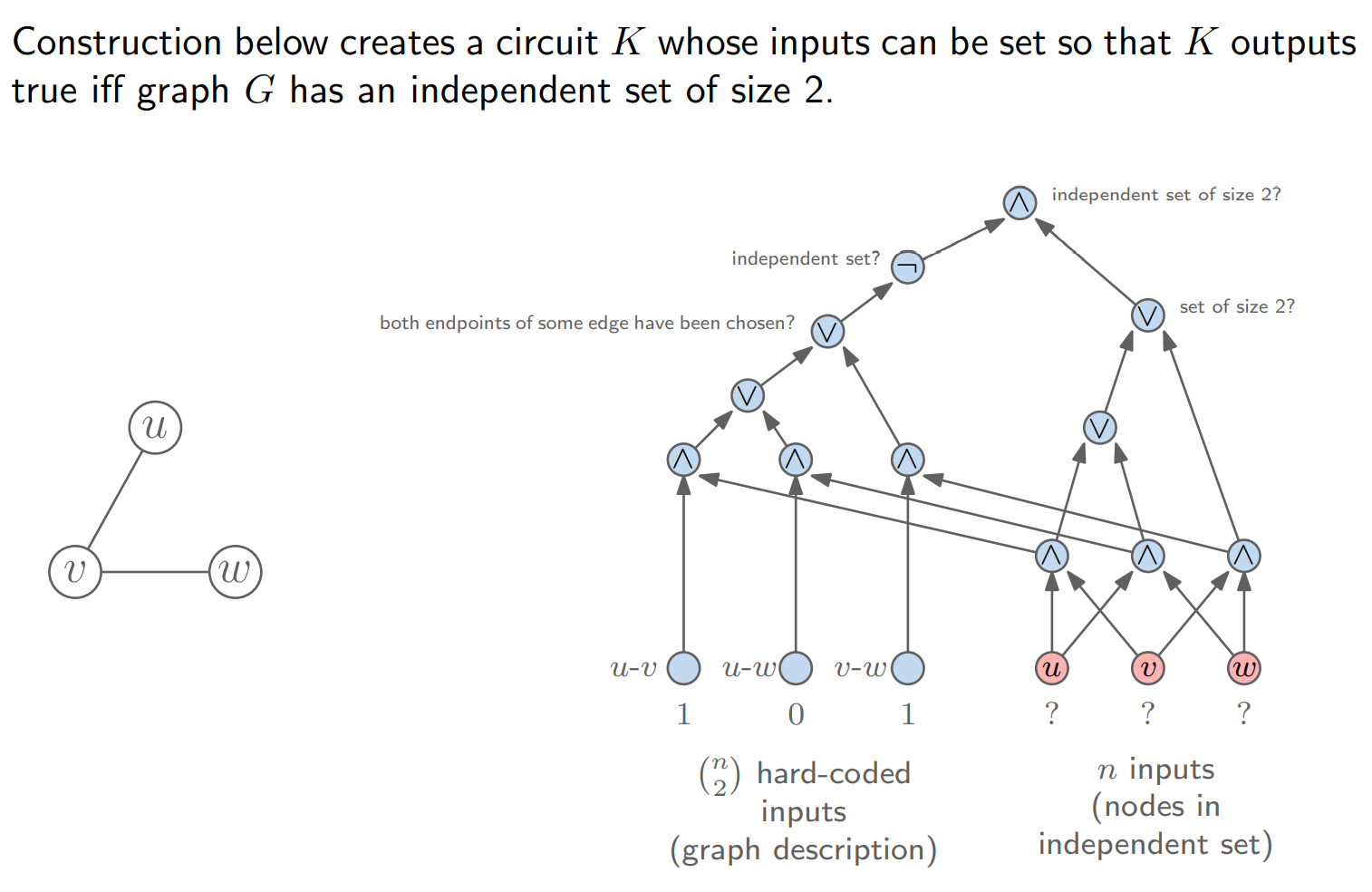
예를 들면, 위와 같은 <Indenpendent Set> 문제에서 왼편의 Graph Instance가 $x$로 hard-coded되어 circuit 입력으로 들어간다. 우리가 찾고자 하는 solution $s$는 circuit에서 비워져 있는 입력값으로 들어가 Circuit-SAT를 푸는 알고리즘을 통해 그 값을 찾아야 한다!
정리하면, 이렇다.
“To solve a problem instance $x \in X$, take a circuit corresponding to $C(x, \cdot)$. Then, use a Circuit-SAT algorithm for this circuit to find a solution (if exist).”
즉, 어떤 Search Problem을 적절한 Circuit-SAT 문제로 바꿔서, Circuit-SAT를 풀면 해당 Search Problem을 풀 수 있는 형태로 환원했다!
이 정리를 통해 <Circuit-SAT>가 $\textbf{NP-complete}$임을 보이게 되고, 이에 따라 <Circuit-SAT> 또는 <SAT>로부터 환원되는 모든 Search Problem들이 $\textbf{NP-complete}$에 속하게 된다! 이 정리를 <Cook–Levin Theorem>라고 하는데, 본 포스트의 증명은 이 정리를 정말 간략하게 기술한 것에 불과하다 🙏
자! 이것으로 “NP & NP-complete” 단원의 내용을 모두 살펴봤다! 현장 수업에서 들을 때도 제일 어려웠던 단원이라 제대로 이해도 못 하고 시험을 봤던 기억이 있다 😢 그래서 알고리즘 수업의 내용을 정리하면, 꼭 정복하고 싶었던 단원을 마무리 하게 되어 뿌듯하다. 이제 마지막 단원만 남겨두었는데, 끝까지 힘내보자 👏
