Green Theorem

복수전공하고 있는 수학과의 졸업시험을 위해 학부 수학 과목들을 다시 공부하고 있습니다. 미적분학 포스트 전체 보기

미적2에서 가장 중요한 챕터가 어디냐고 물으면 바로 “그린 정리”와 “스토스크 정리”다. 사실상 지금까지 배운 미적1과 미적2의 내용은 모두 이 정리를 다루기 위한 빌드업에 불과했단 것… ㅋㅋ 그만큼 이 부분이 중요하고, 이걸 이해하기 위해 그 많은 내용들을 공부한 거라는 사실. 여기까지 이해하기를 포기하지 않고 온게 뿌듯하기도 하다… 🥺 암튼 중요한 내용이기 정신 바짝 차리고 본론으로 ㄱㄱ!

Green Theorem

그린 정리를 한마디로 요약하면 아래와 같다.

어떤 특별한 벡터 함수에 대해, 벡터 선적분과 이중적분을 연결하는 정리.

좀더 정확히 정의하면, 아래 두 적분을 연결하는 졍리다.

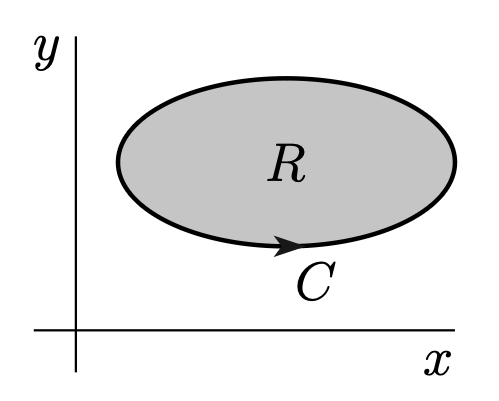
• simple closed curve $C$ 위에서의 벡터 선적분
• 동일한 curve $C$로 정의한 영역 $D$에서의 이중적분

이를 정리의 형태로 서술하면 아래와 같다.

Let $C$ be a positively oriented, piecewise-smooth, simple closed curve in the plane.

Let $D$ be the region bounded by $C$.

If $P$ and $Q$ have continuous partial derivatives on an open region that contains $D$, then

\[\int_C \mathbf{F} \cdot d\mathbf{r} = \int_C P \, dx + Q \, dy = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA\]

Curve Orientation

그린 정리를 기술한 위의 명제에서 “positively oriented”라는 표현이 등장한다. 수학에서는 Curve의 방향을 positive, negative로 정의하는데 CCW 방향을 positive orientation으로 설정한다.

CLP Calculus Textbook

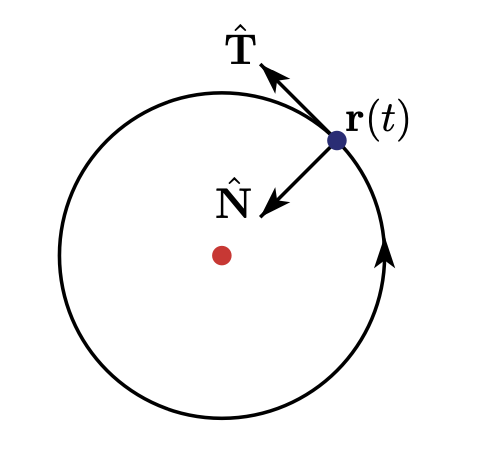
positive orientation을 CCW로 설정하고, TNB 좌표를 잡으면, 법선 벡터 $\mathbf{N}$이 항상 커브 안쪽으로 향하게 된다.

CLP Calculus Textbook

요렇게 말이다!!

Curve Boundary

또, 수학적 표기로 영역 $D$를 감싸하는 positive oriented curve를 편미분 기호를 사용해 아래와 같이 표현한다.

\[\partial D\]

위의 표기를 사용해 그린 정리를 다시 정의하면 아래와 같다.

\[\iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) \, dA = \int_{\partial D} P \, dx + Q \, dy\]

Application of Green Theorem

그린 정리는 경계 위에서의 벡터 선적분과 경계로 만들어지는 영역의 이중적분을 연결하는 정리였다. 이를 활용해

• 벡터 선적분을 계산하기 위해 이중 적분을 수행한다.
• 반대로 이중 적분을 계산하기 위해 벡터 선적분을 수행한다.

이중 적분을 벡터 선적분으로 계산

Find the area enclosed by the ellipse

\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\]

타원의 넓이를 구하는 문제다. 이를 이중 적분으로 정의하면 아래와 같다.

\[\iint_D 1 \, dA\]

이를 그린 정리의 관점에서 보면, $P$, $Q$가 아래 조건을 만족하는 이중 적분을 수행하는 것과 같다.

\[\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1\]

위의 경우를 만족하는 $P$, $Q$는 여러 가지 경우가 하다.

1. $P(x, y) = 0, \, Q(x, y) = x$
2. $P(x, y) = -y, \, Q(x, y) = 0$
3. $P(x, y) = - y / 2, \, Q(x, y) = x / 2$

따라서, 아래의 식이 성립한다.

\[A = \oint_C x \, dy = \oint_C (- y) \, dx = \frac{1}{2} \oint_C x \, dy - y \, dx\]

위의 3가지 방식은 어떤 걸 선택해도 상관 없다 ㅎㅎ (직접 해봄) 제일 쉬울 것 같은, (1)번 방식으로 풀이해보자.

매개화에 의해 $x = a \cos t$, $y = b \sin t$이다. 적분을 치환하면,

\[\begin{aligned} A &= \oint_C x \, dy \\ &= \int_{0}^{2\pi} (a \cos t) (b \cos t) \, dt \\ &= ab \int_{0}^{2\pi} \cos^2 t \, dt \\ &= ab \int_{0}^{2\pi} \frac{\cos 2t + 1}{2} \, dt \\ &= ab \frac{2\pi}{2} = ab \pi \end{aligned}\]

Not simply-connected 영역에서의 적분

그린 정리의 명제를 잘 살펴보면, 곡선 $C$에 대한 조건이 아래와 같이 적혀있다.

positively oriented, piecewise-smooth, simple closed curve

즉, 곡선이 simply-connected인 필요는 없다!!

CLP Calculus Textbook

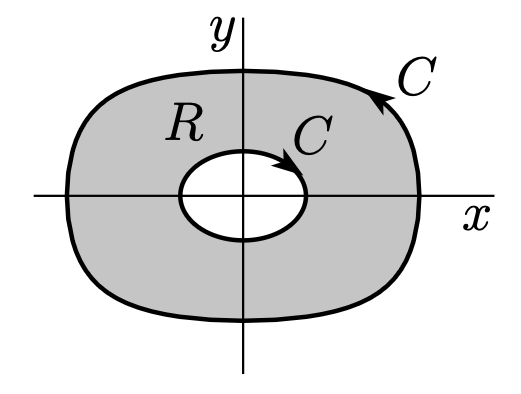
곡선이 요렇게 “도넛 모양“을 이루더라도 그린 정리가 성립한다!! 연습문제를 통해 도넛 형태의 영역을 어떻게 적분할 수 있을지 살펴보자.

(Problem from CLP Calculus Textbook.)

Evaluate

\[\oint_C \mathbf{F} \cdot d\mathbf{r}\]

where

\[\mathbf{F} = \frac{-y \, \mathbf{i} + x \, \mathbf{j}}{x^2 + y^2}\]

and curve $C$ is an unit circle

\[\begin{aligned} x(t) &= \cos t \\ y(t) &= \sin t \end{aligned}\]

[잘못된 풀이] 먼저 그린 정리를 잘못 사용하는 사례부터 살펴보자. 그린 정리에 따라 벡터 선적분을 이중 적분으로 변환하자.

\[\begin{aligned} \oint_C \mathbf{F} \cdot d\mathbf{r} &= \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dA \\ &= \iint_D \left( \frac{-x^2 + y^2}{(x^2 + y^2)^2} - \frac{(-x^2 + y^2)}{(x^2 + y^2)^2}\right) dA = 0 \end{aligned}\]

이중 적분의 값이 0이므로, 벡터 선적분의 값도 0이다…?! 이 풀이는 잘못되었다!!! 그 이유는 이중 적분에서 적분 영역 $D$ 내부에 있는 원점 $O$에서 벡터장 $\mathbf{F}(x, y)$가 정의되지 않기 때문이다. 마찬가지 이유로 원점 $O$에서 1차 편미분 $\partial P$, $\partial Q$도 정의되지 않기 때문에, 그린 정리를 적용하기 위한 전제 조건을 위반한다.

[올바른 풀이] 이런 경우, 적분을 계산하라면 ‘정직하게’ 벡터 선적분 값을 계산하는 수 밖에 없다^^

\[\begin{aligned} \oint_C \mathbf{F} \cdot d\mathbf{r} &= \oint_C P \, dx + Q \, dy \\ &= \int_{0}^{2\pi} \left((- \sin t \cdot - \sin t) + (\cos t \cdot \cos t)\right) \, dt \\ &= \int_{0}^{2\pi} 1 \, dt = 2 \pi \end{aligned}\]

따라서 위의 선적분 값은 $2\pi$이다. 그런데, 이번에는 아래의 문제를 또 풀어보자.

With same vector function, show that $\oint_C \mathbf{F} \cdot d\mathbf{r} = 2\pi$ for every positively oriented simple closed curve that encloses the origin $O$.

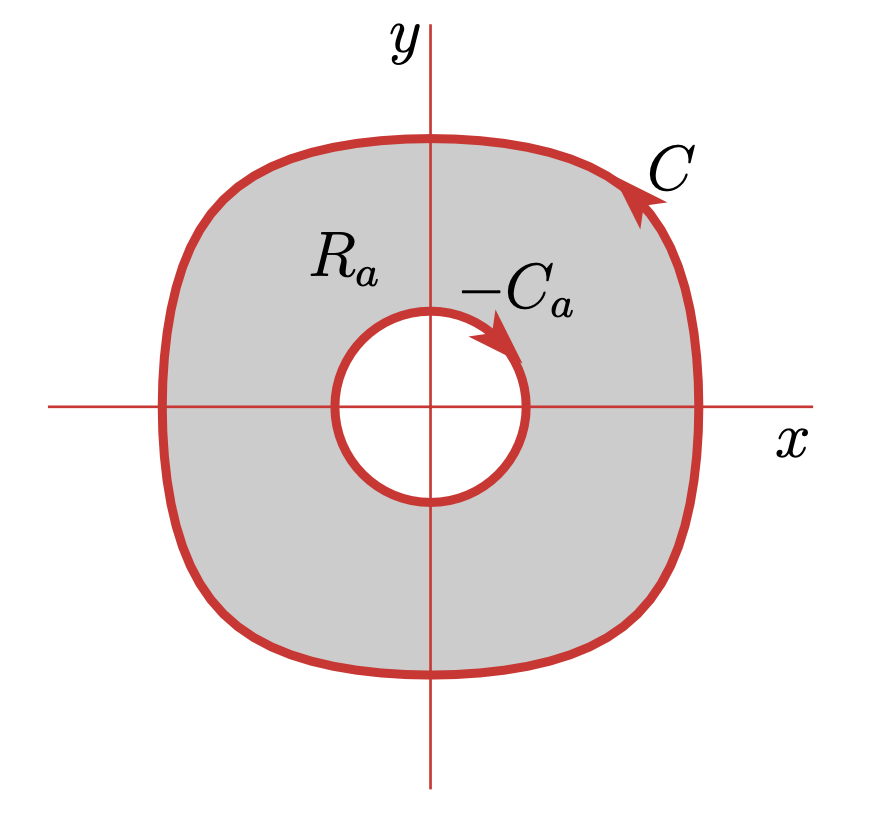
이번에는 원점을 포함하는 “모든” 닫힌 커브에서 선적분 값이 $2\pi$임을 보여야 한다. 이 문제를 풀기 위해선 아래와 도넛 모양의 영역을 상상해야 한다.

CLP Calculus Textbook

$-C_a$는 원점을 중심으로 하는 unit circle이다.

이전과 달리 요런 영역에서는 적분이 가능하다. 원점이 포함되어 있지 않기 때문에 $\mathbf{F}$와 $\partial P$, $\partial Q$가 정의되기 때문 ㅎㅎ 그리고 이에 대한 적분식의 값은 $0$이란건 이미 확인하였다.

\[\iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dA = 0\]

그린 정리의 표기에 따라 적분 영역 $D$의 경계에 대한 선적분으로 이중 적분을 바꿀 수 있다. 이때, 경계 $\partial D$는 CCW의 커브 $C$와 CW 방향의 $-C_a$로 구성된다.

\[\partial D = C + (-C_a)\]

이제 위의 이중 적분 결과를 선적분으로 바꿔서 기술하면,

\[\iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dA = \oint_C \mathbf{F} \cdot d\mathbf{r} + \oint_{-C_a} \mathbf{F} \cdot d\mathbf{r} = 0\]

선적분에 대한 적분만 따로 떼어서 보면,

\[\begin{aligned} \oint_C \mathbf{F} \cdot d\mathbf{r} + \oint_{-C_a} \mathbf{F} \cdot d\mathbf{r} &= 0 \\ \oint_C \mathbf{F} \cdot d\mathbf{r} - \oint_{C_a} \mathbf{F} \cdot d\mathbf{r} &= 0 \\ \oint_C \mathbf{F} \cdot d\mathbf{r} &= \oint_{C_a} \mathbf{F} \cdot d\mathbf{r} = 2\pi \end{aligned}\]

즉, 어떤 닫힌 곡선에 대한 선적분도 모두 unit circle 위에서의 선적분 값과 동일한 $2\pi$가 된다. $\blacksquare$

Partition a Region

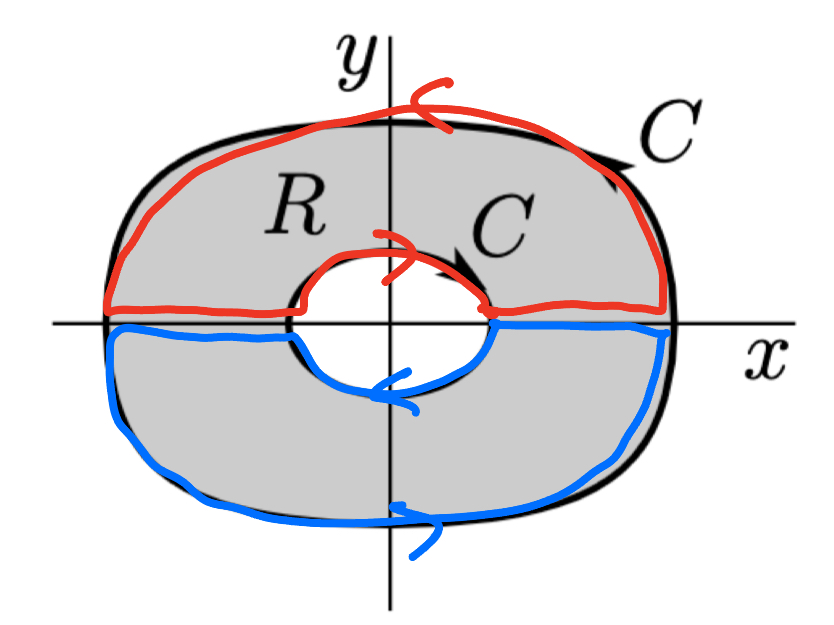
위의 경우는 도넛 모양 영역에 대한 선적분을 이중적분으로 바꿔서 해결한 경우이다. 그런데, 도넛 모양 적분은 아래와 같이 2개의 커브로 분할하여 선적분을 수행할 수도 있다.

CLP Calculus Textbook

요렇게 도넛 영역을 위·아래로 분할하여 2개의 커브로 바꾸어 선적분 하는 것도 가능하다.

맺음말

뭔가 응용복소함수론(MATH210) 수업에서 이런 적분을 많이 했던 기억이 있다. 그때도 닫힌 영역에 대해서 커브의 모양에 상관 없이 적분값이 같은 그런 적분들을 많이 만났던 기억이 난다. 미적2 들을 때, 열심히 들었으면 응복함이 좀더 쉬웠으려냐 ㅠㅠ

이어지는 내용은 미적2의 꽃이라고 할 수 있는 “발산(divergence)와 회전(curl)” 입니다! 그리고 이걸 잘 익히고 나면, 그린 정리를 이 두 연산자를 활용해 기술한 “Vector Form of Green Theorem“을 살펴볼 수 있습니다. 벡터 폼에서는 아래와 같이 2가지 폼이 있습니다.

[Tangential Form]

\[\oint_C \mathbf{F}\cdot d\mathbf{r} = \iint_D \nabla \times \mathbf{F} \, dA = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \, dA\]

[Normal Form]

\[\oint_C \mathbf{F}\cdot \mathbf{N} \, ds = \iint_D \nabla \cdot \mathbf{F} \, dA = \iint_D \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} \right) \, dA\]